Enunciado
Cálculo - Dennis G. Zill - Equações Diferenciais - Vol 1- Ed: 3º - Capítulo 1.2 - Ex. 13
Determine as equações do movimento se o projétil no Problema 12 encontrar uma força de retardamento (de magnitude ) agindo tangencialmente à trajetória mas, oposta ao movimento. Veja a Figura 1.21. [Sugestão: é um múltiplo da velocidade, digamos .]
Passo 1
O movimento do projétil sem a força de retardamento pode ser representado assim:
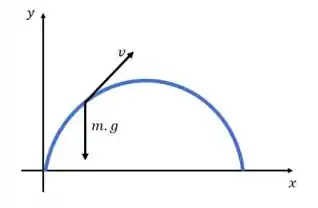
Onde é a velocidade do projétil (tangente à sua trajetória) e é o peso dele.
Mas em situações reais, temos uma força que age também tangencialmente à trajetória mas no sentido contrário ao movimento, assim olha:
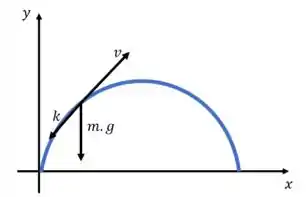
Sendo que é múltiplo de , já que são paralelos.
Podemos, ainda, formar um triângulo retângulo envolvendo e :
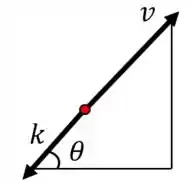
Belezinha, agora que já enxergamos o problema, queremos encontrar um sistema de equações diferenciais pro movimento do projétil, vamos lá!
Passo 2
A segunda lei de Newton nos diz que a força é o produto da massa com a aceleração, ou seja:
Vamos aplicar isso na direção :
Galera, mas sabemos que a aceleração é a segunda derivada da posição não é? Então, podemos escrever assim:
Na direção também temos uma força componente de , que age em direção contrária à trajetória em
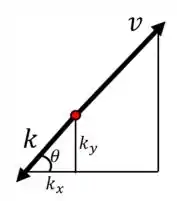
Sendo que
Então:
Como temos que é múltiplo de , vamos escrever (colocamos o módulo na constante , pois caso ela seja negativa, isso mudaria o sentido de , o que não tem sentido físico):
Mas temos que é a componente da velocidade na direção :
Como a velocidade é a derivada da posição:
Passo 3
Agora vamos aplicar a segunda lei de Newton na direção :
Lembrando que a aceleração é a segunda derivada da posição:
A força peso na direção aponta pra baixo e tem valor ., então:
Na direção também temos uma força componente de :
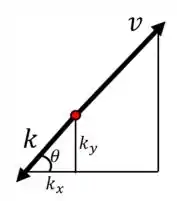
Sendo que
Então:
Vamos escrever :
Mas é a componente da velocidade na direção :
Como a velocidade é a derivada da posição:
Então, as equações que formam o sistema para o movimento do projétil com força de retardamento são: