Determine se existe ou não .

Perceba que a função que nos é dada tem como domínio todos os valores reais: ela é definida por para e vale para .

A partir disso, sabemos já que e o nosso

sacou?

Lembre-se: o e um número muuuuito pequeno, que se aproxima de , mas ele não é , tranquilo? Olha como vai ficar o nosso limite agora:

Simplificando o :

Tranquilo até aqui? 👀

Agora que já temos uma expressão para o nosso limite, temos que analisá-lo e ver se é possível resolvê-lo.

Conforme vai se aproximando de , os valores de vão aumentando, correto? Porque o vai ser dividido por valores cada vez menores de . Logo, a gente pode falar que o tende ao infinito, porque ele vai crescer muuuuuito!

Acontece que a função seno é uma função limitada e periódica: seus valores máximos são e , e ela fica alternando entre esses dois caras. A gente pode ver isso no gráfico abaixo:

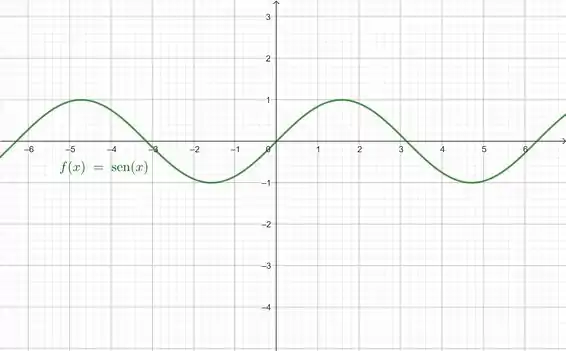
Quem vai ser o seno de um número absurdamente grande então? A resposta é: depende.

Sabemos, por exemplo, que

onde esse aí é um número inteiro (essa propriedade ta relacionada ao círculo trigonométrico, ta bom?). Imagine que , então teríamos que .

Se você pegar a sua calculadora e ver o (que é maior que ), por exemplo, vai ter um número diferente de . Aí se você pegar o , vai dar de novo. Percebeu que não tem um padrão?

Acontece que quando esse número no argumento da função seno cresce, o valor do seno não tende a um número específico, só fica alternando dentro do intervalo . Dá uma olhada no gráfico de como fica (que é a função que apareceu no nosso limite):

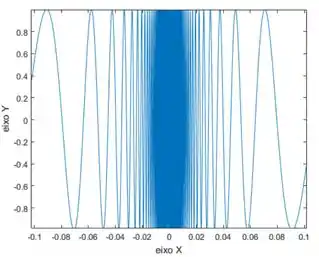
Conforme o vai diminuindo e se aproximando de , a função oscila mais rápido, mas nunca para em um valor fixo, sacou?

Daí a gente conclui que o não existe e, portanto, determinaos que não existe!

E aí! entendeu tudo? Responde Aí! 😎