Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 3.1 - Ex. 67
Seja
é derivável em ? Esboce os gráficos de e
Passo 1
Fala aí, pessoal!
Foi dada a função definida por
e queremos saber se é derivável em 1.
Vejamos, para que uma seja derivável em um ponto dado com , ela deverá ser contínua num intervalo que contenha esse ponto. E podemos ver isso se ela atender a condição abaixo:
Ou seja, o limite da função quando tende ao ponto dado deve ser igual ao valor da função neste mesmo ponto.
Então é isso que faremos, vamos calcular esse limite e ver se ele é igual ao valor da função em .
Partiu!!!
Passo 2
Primeiro vamos calcular:
Mas para que esse limite exista, precisamos que
Ou seja, os limites laterais precisam existe e serem iguais.
Perceba que para valores à esquerda de , isto é, , a função assume a forma
e para valores à direita de , a função tem a forma
Há uma forma de ver essa existência usando a definição de derivada com o limite sendo calculado tanto à esquerda quanto à direita de .
Tranquilo até aqui?
Passo 3
Seja a derivada de com tendendo a 1 pela direita
O limite foi calculado com tendendo pela direita de zero, mas é o mesmo efeito de tendendo pela direita de 1 .
Seja a derivada de com tendendo a 1 pela esquerda
O limite foi calculado com tendendo pela esquerda de zero, mas é o mesmo efeito de tendendo pela esquerda de 1 . Assim, não existe , pois . Desta forma, não é derivável em 1.
Show?
Passo 4
Agora vamos plotar os gráficos para ver melhor isso acontecendo:
para
e
para
Gráficos de e :
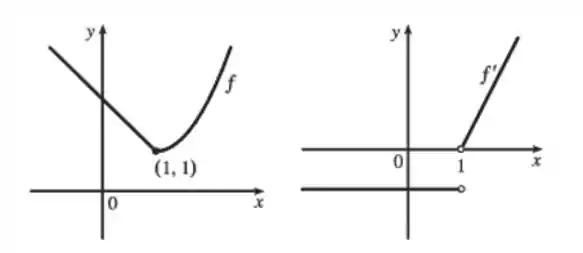
Podemos perceber a descontinuidade da deivada no gráfico a direita.
E aí! O que achou? Responde Aí!
Resposta
não é derivável em 1