Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.7 - Ex. 29
- Se , encontre e use-o para encontrar uma equação da reta tangente à curva no ponto .
- Ilustre a parte (a) traçando a curva e a reta tangente na mesma tela.
Passo 1
E aí galera, tudo bom? Essa aqui é uma questão sobre derivada e reta tangente, um dos tópicos fundamentais de Cálculo e que serve pra muuuuitas outras disciplinas na engenharia! Está preparado para resolver essa questão? Bora lá!
A primeira coisa que temos que ter em mente é que a derivada de uma função qualquer em um ponto é dada da seguinte forma:
Beleza? Essa é a definição de derivada em um ponto e, se esse limite não existir, não teremos a derivada em .
A segunda coisa a termos em mente para a resolução dessa atividade é fórmula da equação da reta tangente:
Em que é o ponto da nossa reta tangente, e nesse caso é o ponto:
De primeira, parece meio complicado trabalhar com essas definições envolvendo limite, é normal, mas é só ir fazendo com calma, resolvendo uns exercícios que dá para ficar fera!
Passo 2
- Primeiro temos que montar nossa expressão para encontrar . Vai ficar assim:
Acontece que, no enunciado, já é dado o valor de para a gente! Presta atenção: sempre escrevemos o par ordenado como sendo e temos um par ordenado Deu para sacar? Temos então que quando , teremos . Bora colocar isso na nossa equação agora:
Já tiramos todas as informações que podíamos do enunciado, agora temos que fazer as contas. Primeiro, temos que ver quem é . Se:
Então:
Fazendo a distributiva e o produto notável:
Simplificando o denominador:
Achamos nosso ! Agora temos que substituir no limite, saca só como vai ficar:
Passo 3
Beleza até aqui? Agora temos que resolver o limite. Uma dica: Tente sempre escrever a sua expressão de uma forma mais amigável, fica mais fácil de visualizar muitas vezes! Vou escrever nosso limite assim:
Sacou? Dividir tudo por é o mesmo que multiplicar por , aí fiz assim para tentar deixar mais organizado. Agora, vamos achar o Mínimo Múltiplo Comum (MMC) entre essa fração de dentro do parêntese e o , dá uma olhada:
Realizando a distributiva:
Vamos fazer a subtração entre as frações agora! Olha só:
Simplificando os termos comuns:
Passo 4
Agora o nosso limite está bem mais organizado! Acontece que, se fizermos a substituição agora para tentar resolver esse limite, vamos cair em uma indeterminação , então temos que dar um jeito de eliminar essa indeterminação. Se eu colocar em evidência na parte de cima da fração, olha só o que vai acontecer:
Simplificando:
Eu eliminei o que estava em evidência com o que estava dividindo. Muitos casos de limite a gente consegue resolver fazendo esse tipo de jogada, então fica com ela na cabeça! Agora vou fazer para tentar resolver nosso limite, dá uma olhada:
Encontramos nosso !
Passo 5
Para terminar o item (a), falta encontrarmos a reta tangente à curva no ponto . Podemos fazer isso utilizando a expressão da reta tangente a um ponto , que é dessa forma aqui:
Nesse nosso caso, temos que e que , beleza? Ah, e tem mais! Encontramos . Temos tudo que é necessário para escrever a equação da reta tangente! Fazendo as substituições, fica assim:
Pronto! Essa é a nossa reta tangente.
Passo 6
b)
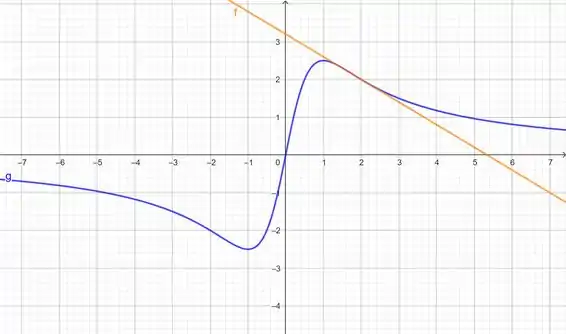
Está quase acabando essa questão! Temos só que desenhar o gráfico da nossa curva e o da reta tangente a ela. Aqui a gente vai utilizar o GeoGebra para fazer isso, pois o intuito é apenas conferir se estamos realmente certos. Vai ficar assim:
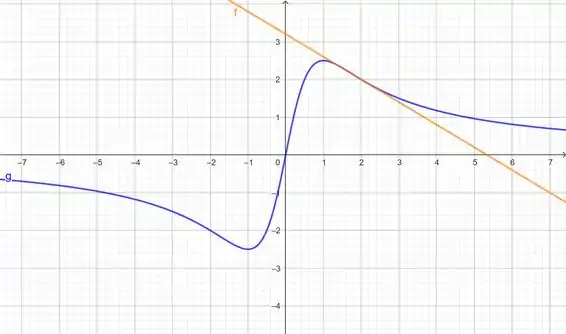
A curva em azul é a curva . Você pode tetnar desenhá-la atribuindo valores e marcando os pontos em um gráfico ou fazendo em um software de computador mesmo.
De posse da curva em azul, você deve desenhar a reta laranja .
Lembre-se: A reta tangente tem que tocar no ponto do gráfico em azul! Esse detalhe é muito importante, pois construímos nossa reta a partir desse ponto, beleza?
Uhul, essa questão já era! ;)
Resposta
- e a reta tangente é .
- O gráfico mostrando a curva e a reta tangente a esta curva no ponto é:
