Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.3 - Ex. 11
Determine e e faça o gráfico de e com domínios e pontos de vista que permitam ver a relação entre eles.
Passo 1
Fala galerinha. De boa? Bora resolver uma questão sobre derivada parcial? 😉
A questão está pedindo para analisar a função
através das suas derivadas parciais e , e depois fazer um gráfico que mostre a função , e de forma que seja perceptível a relação entre elas.
Como fazer isso?
- Podemos começar plotando o gráfico da função .
- Vamos calcular as derivadas parciais; 1º derivar em função de , 2º derivar em função de .
- Interpretar as derivadas parciais: Entender como e variam em relação às mudanças em e , respectivamente. Isso pode indicar a taxa de variação da função nas direções de e .
- Fazer o gráfico utilizando um software (Desmos por exemplo) com pontos que mostram relação entre si.
- Representar o domínio da função.
Vamos começar a resolver! 😊
Passo 2
Primeiro vamos plotar o gráfico de , assim podemos ir comparando.
Para , temos:
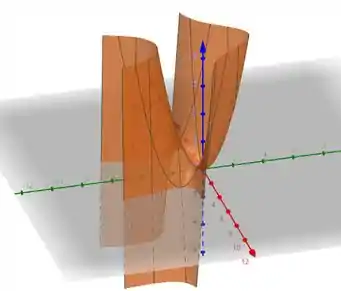
No gráfico a direção das parábolas formadas no gráfico de nos eixos e são correlacionadas com o crescimento e decrescimento dos gráficos de e .
Passo 3
Agora vamos resolver , para isso devemos derivar em relação a .
Vamos considerar como fixo
Seu gráfico fica:
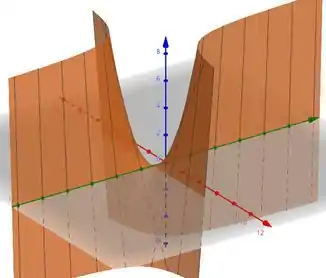
Perceba que no gráfico de vemos uma parábola crescendo na direção do essa parábola vira uma função do terceiro grau para o crescimento de na direção do mesmo eixo.
Passo 4
Agora vamos resolver , para isso devemos derivar em relação a .
Vamos considerar como fixo
Seu gráfico fica:
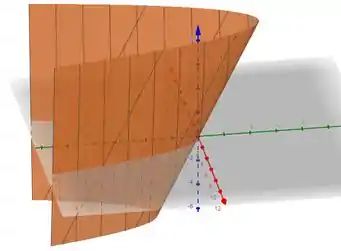
Uma coisa legal de se notar é pelo gráfico de que vemos que esse gráfico corta o plano no ponto de e esse ponto é um ponto de mínimo da função f.
Passo 5
Vamos comprar agora? Será rápido!
A função apresenta um mínimo no ponto e cresce em todas as direções devido aos termos e . O termo adiciona uma deformação.
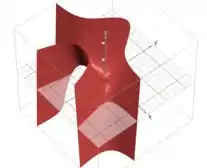
A derivada parcial mostra uma inclinação que depende tanto de quanto de . A presença de indica que a taxa de mudança em é influenciada pelo valor de .
A derivada parcial , a inclinação é principalmente determinada por e cresce quadraticamente em , devido ao termo . Isso significa que a variação em é mais rápida onde é maior.
Passo 6
Domínio da função :
A função está definida para todos os valores reais de e . Portanto, seu domínio é, ou seja, todos os pares ordenados pertencentes ao plano cartesiano.
Resposta
Passos acima.