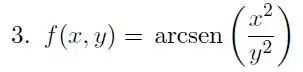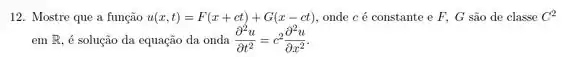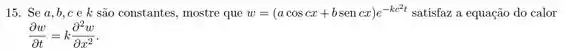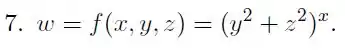Exercícios de Derivadas Parciais - Lista de Exercícios Resolvida
Questão 1
Determine as derivadas parciais em relação a e a , para a seguinte função:
Ver solução completaQuestão 2
Seja , em que é uma função diferenciável de uma variável real. Verifique que
Ver solução completaQuestão 6
Seja , em que é uma função diferenciável de uma variável real. Verifique que
para todo com .
Ver solução completaQuestão 7
Seja , em que é uma função diferenciável de uma variável real. Verifique que
Ver solução completaQuestão 9
A função é diferenciável no plano. Definimos Obtenha a expressão em termos de (Lembre-se que
Ver solução completaQuestão 13
6.1) Seja uma função com derivadas parciais contínuas e suponha que a equação define como uma função diferenciável de e , ou seja, . Mostre que
Nos pontos nos quais , em que indica a derivada parcial de em relação à segunda variável.
Ver solução completaQuestão 20
4) Determine a aproximação linear da função em e use-a para aproximar o número .
Ver solução completaQuestão 21
3) Considere a superfície dada pela equação . Se o vetor é tangente a em , mostre que
Ver solução completaQuestão 37
Utilizar a definição para encontrar cada uma das derivadas parciais:
a)
Ver solução completaQuestão 38
Utilizar a definição para encontrar cada uma das derivadas parciais:
c)
Ver solução completaQuestão 39
Utilizar a definição para encontrar cada uma das derivadas parciais:
d)
Ver solução completaQuestão 40
Encontre as derivadas parciais, como se fossem derivadas ordinárias, considerando constantes todas menos uma das variáveis.
(2)
Ver solução completaQuestão 41
Encontre as derivadas parciais, como se fossem derivadas ordinárias, considerando constantes todas menos uma das variáveis.
(1)
Ver solução completaQuestão 42
4] Encontre as derivadas parciais, como se fossem derivadas ordinárias, considerando constantes todas menos uma das variáveis
(6)
Ver solução completaQuestão 43
4] Encontre as derivadas parciais, como se fossem derivadas ordinárias, considerando constantes todas menos uma das variáveis
(7)
Ver solução completaQuestão 44
4] Encontre as derivadas parciais, como se fossem derivadas ordinárias, considerando constantes todas menos uma das variáveis
(8)
Ver solução completaQuestão 45
5] Encontrar as derivadas parciais correspondentes em cada caso
(2) ;
Ver solução completaQuestão 46
5] Encontrar as derivadas parciais correspondentes em cada caso
(3) ;
Ver solução completaQuestão 50
Considere a função
- A função é contínua em Justifique sua resposta.
- Calcule as derivadas parciais e
- Determine e para .
- é diferenciável em ? Justifique sua resposta.
Questão 51
11 - Numa circunferência de raio , traçam-se duas cordas paralelas, uma acima e outra abaixo do centro, e constrói-se um trapézio isósceles. Determine as distâncias das duas cordas ao centro para que a área do trapézio seja máxima.
Ver solução completaQuestão 53
Uma condição suficiente para que a fórmula
Ser verdadeira é que seja ..... em .
Ver solução completaQuestão 54
Dados os valores observados de uma quantidade em torno dos valores médios e :
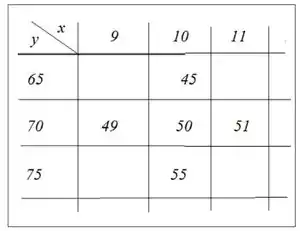
- Estime as taxas de variação de com e de com em torno dos valores médios.
- Determine a aproximação linear de em torno do ponto médio
Questão 55
4 – O índice de sensação térmica é modelado pela função
Onde é a temperatura (em ) e é a velocidade do vento (em ). Às 15:30h num determinado lugar de Niterói, no dia 26 de janeiro de 2023, se medem , com possível erro de e com possível erro de . Estime o erro máximo cometido no valor calculado de em decorrência dos erros de e . Calcule aproximadamente para e usando a estimativa para o erro máximo.
Ver solução completaQuestão 56
Seja , em que é uma função diferenciável de uma variável real. Mostre que .
Ver solução completaQuestão 59
4) Dada a função . Arraste e solte nas lacunas, as respectivas derivadas parciais da função:
a)
b)
Ver solução completaQuestão 64
Sendo encontre a soma das derivadas parciais da função em relação a cada variável no ponto .
Questão 65
Se resistores elétricos de , , ohms são conectados em paralelo para formar um resistor de ohms, o valor de pode ser encontrado a partir da equação:
Encontre o valor de quando , e ohms.
Ver solução completaQuestão 68
Utilizar a definição para encontrar cada uma das derivadas parciais:
b)
Ver solução completaQuestão 70
Encontre as derivadas parciais, como se fossem derivadas ordinárias, considerando constantes todas menos uma das variáveis.
(4)
Ver solução completaQuestão 71
4] Encontre as derivadas parciais, como se fossem derivadas ordinárias, considerando constantes todas menos uma das variáveis
(5)
Ver solução completaQuestão 75
Considere a função , em que é uma função real de uma variável diferenciável. Verifique se vale a seguinte equação:
Ver solução completaQuestão 76
Considere a função , onde é uma função real de uma variável, diferenciável em todo , sendo e constantes. Verifique que para todo :
Ver solução completaQuestão 79
6] Dada a função . Verifique se satisfaz a equação diferencial em derivadas parciais,
Ver solução completaQuestão 81
13] Mostre que , onde é uma função diferenciável arbitrária, é uma solução geral da equação em derivadas parciais
Ver solução completaQuestão 83
14] Mostre que é uma solução geral da equação em derivadas parciais,
Também encontre a solução particular satisfazendo as condições , , .
Ver solução completaQuestão 91
11 - Determine o maior conjunto aberto no qual nos seguintes casos:
c) .
Ver solução completaQuestão 97
Considere a equação que define implicitamente em função de . Usando a fórmula temos:
Questão 101
Sejam , . Determine e de duas maneiras:
- Expressando em termos de e s
Questão 102
Seja
O que aconteceu para que as derivadas mistas não fossem iguais?
Ver solução completaQuestão 103
7 - A janela de uma casa tem a forma de um retângulo com um triângulo isósceles no topo. Se o perímetro da janela é e esta deve coletar a maior quantidade de energia solar possível, mostre que o ângulo da base do triângulo é radianos.
Ver solução completaQuestão 104
(Cap 14.3 – Ex 11) Se , encontre e interprete esses números como inclinações. Ilustre com esboços desenhados à mão ou gráficos de computador.
Ver solução completaQuestão 105
(Cap 14.3 – Ex 96c) No estudo de penetração do congelamento descobriu-se que a temperatura no instante (medido em dias) a uma profundidade (medida em pés) pode ser modelada pela função
onde e é uma constante positiva.
(c) Mostre que satisfaz a equação do calor para uma certa constante .
Ver solução completaQuestão 106
(Cap 14.3 – Ex 45) Use a definição de derivadas parciais como limites (4) para encontrar e .
Ver solução completaQuestão 107
A energia cinética de um corpo com massa e velocidade é . Nestas condições a afirmação é verdadeira ou falsa?
Ver solução completaQuestão 108
A lei dos gases para uma massa fixa m de um gás ideal à temperatura absoluta T, pressão P e volume é dada por , nesta fórmula R é a constante do gás. Nestas condições a afirmação:
É verdadeira ou falsa?
Ver solução completaQuestão 109
A altura de ondas em mar aberto depende da velocidade do vento e do tempo durante o qual o vento se manteve naquela intensidade. Os valores da função são apresentados na tabela abaixo:
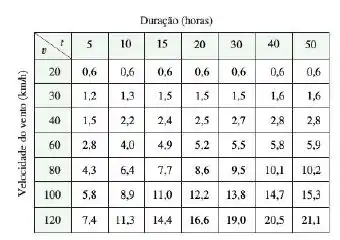
- Qual o significado das derivadas parciais e ?
- Estime os valores de e . Quais são as interpretações práticas desses valores?
- Qual parece ser o valor do limite ?
Questão 110
16] De acordo com a lei de gases ideais para um gás confinado, Se for a pressão, unidades cúbicas o volume e graus a temperatura, temos
onde é uma constante de proporcionalidade. Mostre que
Ver solução completaQuestão 111
17] A temperatura em qualquer ponto de uma placa é graus, e
Se a distância for medida em polegadas, encontre no ponto a taxa de variação da temperatura em relação à distância na placa na direção do eixo positivo e na direção do eixo positivo.
Ver solução completaQuestão 112
Questão 3. calcule o rotacional e divergente dos seguintes campos de vetores.
(a) ;
Ver solução completaQuestão 113
Questão 3. calcule o rotacional e divergente dos seguintes campos de vetores.
(c) ;
Ver solução completaQuestão 114
Questão 3. calcule o rotacional e divergente dos seguintes campos de vetores.
(b) ;
Ver solução completaQuestão 115
Determine a taxa de variação máxima de
no ponto e a direção em que isso ocorre.
Ver solução completaQuestão 116
Um arco não regular. Seja o arco dado por: , e . Note que a coordenada do arco é:
Com derivada , para e .
Sendo esta derivada descontínua em , concluímos que o caminho não é regular.
Ver solução completaQuestão 120
Verifique que a função é solução da equação de Laplace bidimensional
Ver solução completaQuestão 122
Questão 3. calcule o rotacional e divergente dos seguintes campos de vetores.
(d) ;
Ver solução completaQuestão 124
(Cap 14.3 – Ex 17) Determine as derivadas parciais de primeira ordem da função.
Ver solução completaQuestão 128
(Cap 14.3 – Ex 6) Determine os sinais das derivadas parciais da função f cujo gráfico é mostrado
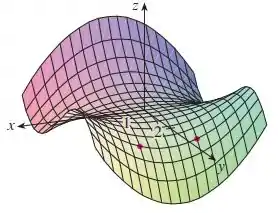
Questão 129
Suponha que a função diferenciável satisfaça para todo .
Calcule sabendo que .
Ver solução completaQuestão 142
Determine os pontos da superfície que estão mais próximos e mais distantes da origem, isto é, de .
Ver solução completaQuestão 143
Determine o ponto sobre o gráfico da função onde o plano tangente é paralelo a plano . Determine também a equação do plano tangente.
Ver solução completaQuestão 144
Dada a superfície de equação , para quais valores positivos de e o seu plano tangente no ponto é paralelo ao plano .
Ver solução completaQuestão 147
11 - Determine o maior conjunto aberto no qual nos seguintes casos:
b) ;
Ver solução completaQuestão 148
10 - Uma função com segundas derivadas parciais contínuas que satisfaz a Equação de Laplace é dita harmônica. Qual das funções abaixo são harmônicas?
b) ;
Ver solução completaQuestão 149
11 - Determine o maior conjunto aberto no qual nos seguintes casos:
a) ;
Ver solução completaQuestão 153
As dimensões de uma caixa retangular fechada foram medidas como e , respectivamente, com erro máximo de em cada dimensão. Utilize diferenciais para estimar o máximo percentual de erro no cálculo da área da superfície da caixa
Ver solução completaQuestão 155
Considerando que a equação define como uma função de , encontre o valor de no ponto
Ver solução completaQuestão 156
Sejam e um vetor unitário
- Mostre que é continua a pesar de não ser diferenciável.
- As derivadas parciais de são contínuas na origem.
Questão 157
10 - Uma função com segundas derivadas parciais contínuas que satisfaz a Equação de Laplace é dita harmônica. Qual das funções abaixo são harmônicas?
a) ;
Ver solução completaQuestão 158
Próximo a uma bóia, a profundidade de um lago com coordenadas é , onde e são dados em metros. Um pescador que está em um pequeno barco parte do ponto em direção à bóia, que está localizada no ponto . A água sob o barco está ficando mais profunda ou mais rasa quando ele começa a se mover? Explique.
Ver solução completaQuestão 159
Considere a função
Desenhe as curvas contidas no conjunto
E no conjunto
Apontando no desenho o conjunto e o conjunto .
Ver solução completaQuestão 160
Calcule as derivadas parciais em relação à de primeira e segunda ordens da função dada
Ver solução completaQuestão 161
Quando f (x) derivável quando x = a, a variação aproximada do valor de f, quando x varia de a para a + △x é dado pelo diferencial total avaliado no ponto x = a, ou seja,
(variação da linearização de f correspondente à variação dx = △x). Use diferenciais para aproximar os números e . Essas aproximações estão superestimadas ou subestimadas?
Ver solução completaQuestão 163
(2) Seja
c) Generalizando b) acima, calcule as derivadas parciais em todos os pontos em que .
Ver solução completaQuestão 164
Calcule as derivadas parciais em relação à de primeira e segunda ordens da função dada
Ver solução completaQuestão 168
Seja onde é uma função diferenciável. Determine h’(t) em função das derivadas parciais de f. Sabendo que encontre .
Ver solução completaQuestão 169
Calcule as derivadas parciais em relação à de primeira e segunda ordens da função dada
Ver solução completaQuestão 170
Calcule as derivadas parciais em relação à de primeira e segunda ordens da função dada
Ver solução completaQuestão 178
Utilize a Regra da Cadeia para determinar as derivadas parciais indicadas.
b)
quando
Ver solução completaQuestão 179
A temperatura em um ponto é , medida em graus Celsius. Um inseto rasteja, de modo que sua posição após segundos é dada por , onde e são medidos em centímetros. A função da temperatura satisfaz e . Quão rápido a temperatura aumenta no caminho do inseto depois de três segundos?
Ver solução completaQuestão 185
24 Seja .
(a) Encontre o coeficiente angular da reta tangente à curva que está na intersecção do gráfico de com o plano , no ponto .
Ver solução completaQuestão 186
Identificar as afirmações verdadeiras
A união de bolas abertas é uma bola aberta.
Ver solução completaQuestão 187
Seja uma função harmônica no aberto , ou seja, , para todo . Sejam ainda funções de classe no aberto tais que para todo e satisfaçam e .
Mostre que .
Ver solução completaQuestão 190
Calcule as derivadas parciais em relação à de primeira e segunda ordens da função dada
Ver solução completaQuestão 191
Calcule as derivadas parciais em relação à de primeira e segunda ordens da função dada
Ver solução completaQuestão 192
Calcule as derivadas parciais em relação à de primeira e segunda ordens da função dada
Ver solução completaQuestão 193
Calcule as derivadas parciais em relação à de primeira e segunda ordens da função dada
Ver solução completaQuestão 194
Calcule as derivadas parciais em relação à de primeira e segunda ordens da função dada
Ver solução completaQuestão 195
Calcule as derivadas parciais em relação à de primeira e segunda ordens da função dada
Ver solução completaQuestão 196
Calcule as derivadas parciais em relação à de primeira e segunda ordens da função dada
Ver solução completaQuestão 197
Calcule as derivadas parciais em relação à de primeira e segunda ordens da função dada
Ver solução completaQuestão 198
Calcule as derivadas parciais em relação à de primeira e segunda ordens da função dada
Ver solução completaQuestão 199
Calcule as derivadas parciais em relação à de primeira e segunda ordens da função dada
Ver solução completaQuestão 200
Calcule as derivadas parciais em relação à de primeira e segunda ordens da função dada
Ver solução completaQuestão 201
Calcule as derivadas parciais em relação à de primeira e segunda ordens da função dada
Ver solução completaQuestão 202
Calcule as derivadas parciais em relação à de primeira e segunda ordens da função dada
Ver solução completaQuestão 203
Calcule as derivadas parciais em relação à de primeira e segunda ordens da função dada
Ver solução completaQuestão 204
5] Encontrar as derivadas parciais correspondentes em cada caso
(1) ;
Ver solução completaQuestão 205
Encontre as derivadas parciais, como se fossem derivadas ordinárias, considerando constantes todas menos uma das variáveis.
(3)
Ver solução completaQuestão 209
(b) Verifique que satisfaz a equação de Laplace
sendo . (Uma função que satisfaz a equação de Laplace é chamada harmônica.)
Ver solução completaQuestão 213
Utilize a Regra da Cadeia para determinar as derivadas parciais indicadas.
a)
quando
Ver solução completaQuestão 214
Utilize a Regra da Cadeia para determinar as derivadas parciais indicadas.
c)
quando
Ver solução completaQuestão 217
Sabe-se que é diferenciavel em R² e que o gráfico de f contém as imagens de ambas as curvas e . Determine , onde .
Ver solução completa