Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.4 - Ex. 36a
Determine se a função dada é par, ímpar ou nenhuma das duas.
Passo 1
Da definição, sabemos que uma função par é uma que seja espelhada no eixo , como uma parábola. E uma função ímpar é uma função também espelhada, porém invertida. A rigor podemos definir uma função par como uma função que satisfaz:
E uma função é dita ímpar se ela satisfaz:
Se a função não satisfizer nenhuma das duas condições ela não é par nem ímpar! Vamos checar para cada caso para a função acima.
Passo 2
Vamos começar assumindo que
Como o polinômio só tem termos com expoentes pares, realmente, e . Assim provamos que a nossa função é par!
Passo 3
Saca só o gráfico dessa função:
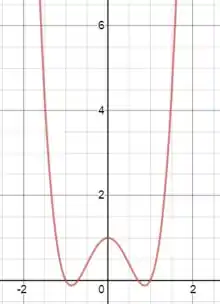
Realmente ela possui simetria par! O mesmo acontece para qualquer polinômio que só tenha termos com expoentes pares.
Resposta
Par
Exercícios de Livros Relacionados
Determine se a função dada é par, ímpar ou nenhuma das duas. f x = x 3 + 1
Determine se a função dada é par, ímpar ou nenhuma das duas. f z = z - 1 2
Determine se a função dada é par, ímpar ou nenhuma das duas. f s = s 2 + 2 s + 2
Determine se a função dada é par, ímpar ou nenhuma das duas. f x = 1 ,s ex0 - 1 ,s ex0