Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.6 - Ex. 74
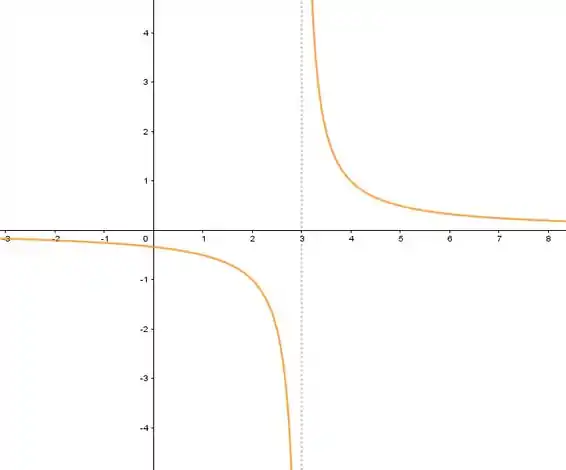
Determine uma função que satisfaça as condições dadas e trace seu gráfico.
, e
Passo 1
O primeiro passo é olhar o tipo de resposta que o limite apresenta, ou seja, se zero, um número ou . Com isso, nós podemos ver qual tipo de função se encaixa melhor para cada caso.
Na questão temos que, , isso significa que uma divisão de polinômios, onde o grau do polinômio de baixo fosse maior que grau o do polinômio de cima, cairia bem já que nesses casos, quando o limite dará . Veja no exemplo abaixo:
Passo 2
O segundo passo é perceber quee isso quer dizer que em , tem um “probleminha”. Com isso, temos que provavelmente é uma divisão de polinômios, que quando substituímos o denominador zera.
Dessa forma,
O que é TOP pois,
E,
Além disso,
Isso acontece pois estamos considerando então o resultado será negativo.
Resposta
