Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.4 - Ex. 3
Determine uma janela retangular apropriada para a função dada e use-a para fazer o gráfico da função.
Passo 1
A questão pede para fazermos um esboço do gráfico da função na janela apropriada.
Para determinar uma janela retangular apropriada para o gráfico da função, precisamos considerar alguns aspectos importantes:
1. Comportamento da Função:
- Extensões: É importante identificar os valores máximo e mínimo da função no intervalo de interesse para definir os limites da janela.
- Pontos de interesse: Se a função possui pontos específicos de interesse, como raízes, pontos de inflexão ou assíntotas, a janela deve ser ajustada para capturá-los.
2. Escala e Proporção:
- Visibilidade: A janela deve ser dimensionada de forma que o gráfico da função seja visível e compreensível.
- Proporção: A proporção da janela (largura/altura) deve ser adequada à forma da função para evitar distorções no gráfico.
Nesse caso, temos que levar em consideração alguns pontos importantes para essa função. Aqui, temos uma equação do segundo grau, sendo assim, os pontos importantes para ela são suas raízes, e o seu vértice.
Já que a janela retangular apropriada deve nos mostrar os pontos mais importantes do gráfico, para que tenhamos uma melhor compreensão do comportamento da função, devemos nessa questão escolher uma região que contenham esses pontos.
Passo 2
Vamos começar a nossa analise então encontrando as raízes da função:
Então 2 pontos importantes a gente já tem. Agora vamos atrás do vértice da função. O vértice de uma função do segundo grau é dada por:
Vamos então as susbstituições:
Sendo assim, temos o ponto onde a nossa função possui seu valor máximo:
Passo 3
Com os dados do passo 2 em mãos, podemos então escolher uma janela. Veja que precisamos poder ver com detalhes todos os pontos que citamos anteriormente, as raízes e o vértice.
Vamos então utilizar uma janela , ela é maior que o os nossos pontos e permite que os vejamos com definição:
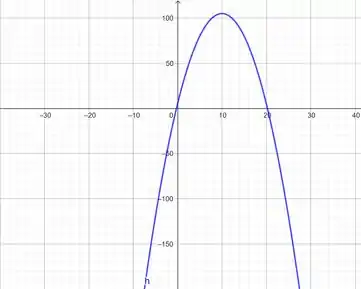
E é isso meu amigo. Forte abraço e até uma próxima.
Resposta
Esboço de gráfico.