Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.4 - Ex. 12
Determine uma janela retangular apropriada para a função dada e use-a para fazer o gráfico da função.
Passo 1
Olá, amigo! Hoje vou te auxiliar a completar este exercício.
O exercício solicita que identifiquemos a janela retangular adequada para a função fornecida. Mas o que isso realmente significa?
Quando usamos uma calculadora gráfica ou um computador muito potente, a visualização do gráfico acontece dentro de um espaço retangular, não mostrando o gráfico inteiro. Esse espaço, onde o gráfico é exibido, é conhecido como janela de visualização, tela de observação ou janela retangular.
Então para construirmos uma janela retangular apropriada, deveremos assim como as calculadoras gráficas, encontrarmos a variação de de até e os valores de de até , e nossa parte visível do gráfico será o retângulo:
Que pode ser vista abaixo como:
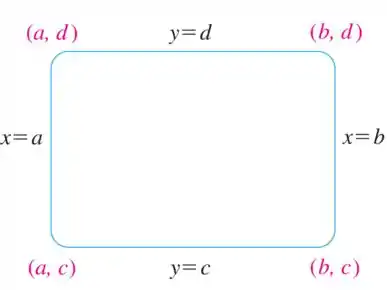
Uma forma de encontrarmos a janela retangular é analisarmos o domínio e a imagem da função. E a partir daí encontrarmos os valores . E é isso que iremos fazer aqui.
Passo 2
Temos então a função
Podemos reescrever essa função como
Uma forma de encontrarmos a janela retangular é analisarmos o domínio e a imagem da função. Para essa função, vemos que o denominador não pode ser nulo, sendo assim:
Uma função possui seus zeros em
Sendo pertencente aos números inteiros.
Então para a nossa função:
Simplificando os
Dividindo por :
Sendo assim, o domínio de
É
Então já sabemos qual região é importante para o gráfico no que diz respeitos aos seus pontos de indefinição.
Vamos agora analisar o conjunto imagem da função, ele irá nos ajudar a definirmos os limitantes de .
Ao analisar a função
Note que
É limitada no intervalo
Isso faz com que o menor valor positivos e negativos, respectivamente sejam , mas sem limitações superiores. Sendo assim, o conjunto imagem é
Passo 3
Outro ponto importante para o gráfico é o período da função que nos foi dada. A função é periódica e tem seu período de Isso quer dizer que a cada os valores da função irão se repetir.
Veja que, ao encontrarmos o período de também iremos encontrar um ponto importante sobre o qual poderemos melhor construirmos o gráfico da função.
é o resultado de contrair horizontalmente por um fator de . O período de é .
Como possui um período de , sugiro que podemos usar um intervalo para duas oscilações, que é . Temos então os pontos de indefinição da função que encontramos no passo 2,
E agora temos nosso limitante em . Vamos aos gráficos.
Passo 4
Veja bem, agora iremos procurar de fato um trecho do gráfico que consiga melhor representar o gráfico que queremos. Iremos fazer isso a partir da análise que fizemos da janela retangular.
Para construção dos gráficos irei utilizar o GeoGebra, mas fique à vontade para utilizar o software de sua preferência.
Primeiro vamos visualizar com apenas uma oscilação, e para o limitante em vamos utilizar , pois é um intervalo que conseguimos visualizar os pontos mínimos da nossa imagem.
Para a janela:
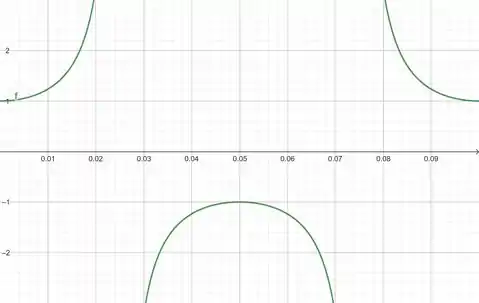
Agora vamos visualizar com duas oscilações e ampliarmos a visualização em .
Para a janela:
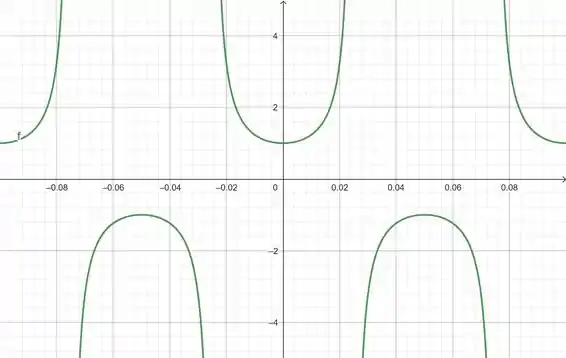
Veja que no intervalo
Podemos visualizar melhor o comportamento do gráfico da função, sendo assim esse será o escolhido.