Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.4 - Ex. 9
Determine uma janela retangular apropriada para a função dada e use-a para fazer o gráfico da função.
Passo 1
Eaee, belezinha?? Bom... a questão pede para determinarmos uma janela retangular adequada para a seguinte função:
Em seguida, devemos esboçar o gráfico nessa janela.
Lembre-se que janela retangular adequada para uma função em geral refere-se a uma região retangular no plano que é suficientemente grande para conter a curva da função.
Mas não é tão grande a ponto de incluir uma área desnecessária.
Para isso, uma ideia é compararmos com uma função parecida e analisar as mudanças.
Bora lá!! 😉
Passo 2
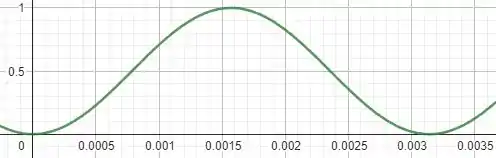
Perceba que a função se parece muito com a função seno, mas temos duas diferenças.
A primeira é que o seno está elevado ao quadrado. Dessa forma, a nossa função não apresenta valores negativos de .
Assim, podemos excluir a parte negativa de da nossa janela retangular.
A outra diferença é o argumento da função sendo, que é , isso significa que a frequência da oscilação aumenta, fazendo com que o período diminua em vezes.
Assim, a nossa janela retangular seria reduzida em vezes no eixo .
Passo 3
Dessa forma, com as informações apresentadas no passo 2, temos que a janela é uma janela retangular apropriada para a nossa função, veja:
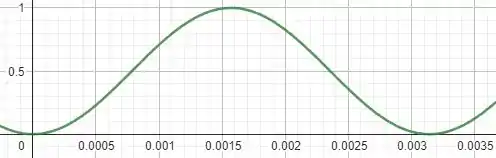
Resposta
