Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.4 - Ex. 26
Use os gráficos para determinar qual das funções e é, eventualmente, maior.
Passo 1
O problema fornece duas funções:
E queremos plotar o gráfico de ambas para ver qual delas é maior.
Podemos reparar que uma função é um polinômio de quarto grau e outra função é um polinômio de terceiro grau.
Passo 2
A seguir plotamos as duas curvas:
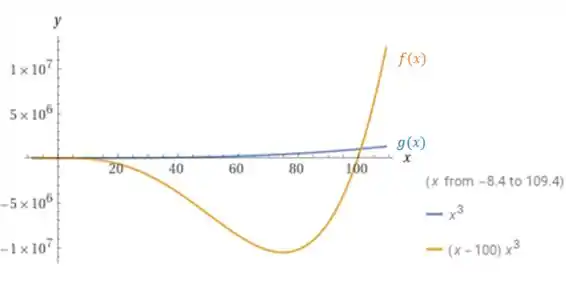
Vemos que para grande ), a função ultrapassa a função .
Dessa forma, podemos dizer que para , a função é eventualmente maior.
Resposta
Exercícios de Livros Relacionados
Faça o gráfico da função: y = sqrt(| x |)
Suponha que f seja uma função par, g seja uma função ímpar e tanto f como g sejam definidas na reta real ℝ. Quais das seguintes funções (quando definidas) são pares? E ímpares? a )f g
Faça o gráfico da função: y =1 2 x - 1 Comece pelo gráfico de uma das funções padrão apresentadas nas figuras 1.14-1.17 e aplique a mudança adequada.
Seja f ( x ) = x - 7 e g ( x ) = x ² ². Faça o gráfico de f e g juntamente com f @ g e g @ f .
O exercício a seguir apresenta uma equação de elipse. Coloque a equação no formato padrão e esboce a elipse. 3 x - 1 2 + 2 y + 2 2 = 6