Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.2 (exercícios de compreensão) - Ex. 3
O gráfico de pode ser obtido transladando o gráfico de para a __________ (esquerda/direita) por __________ unidade(s) e depois transladando o novo gráfico para __________ (cima /baixo) por _________ unidade(s).
Passo 1
Temos que completar a frase:
O gráfico de pode ser obtido transladando o gráfico de para a __________ (esquerda/direita) por __________ unidade(s) e depois transladando o novo gráfico para __________ (cima /baixo) por _________ unidade(s).
Para isso, vamos lembrar da tabela 0.2.2 só:
Se diminuímos de uma constante positiva (ex.: ), transladamos o gráfico para a direita. Se, ao invés de diminuir, somarmos (ex.:), transladamos para a esquerda, ok?
Se a gente faz isso para é o contrário: quando somamos uma constante positiva (ex.:), o gráfico sobe. E, quando subtraímos (ex.:), o gráfico desce.
Passo 2
Com isso, como temos , podemos pensar que, inicialmente, tínhamos . E o que fizemos? Subtraímos no , deslocando o gráfico para a direita, e somamos no , deslocando o gráfico para cima.
Então, a frase preenchida seria:
O gráfico de pode ser obtido transladando o gráfico de para a (direita) por () unidade(s) e depois transladando o novo gráfico para (cima) por () unidade(s).
Quer dar uma olhada no antes e depois? Se liga só:
Antes, :
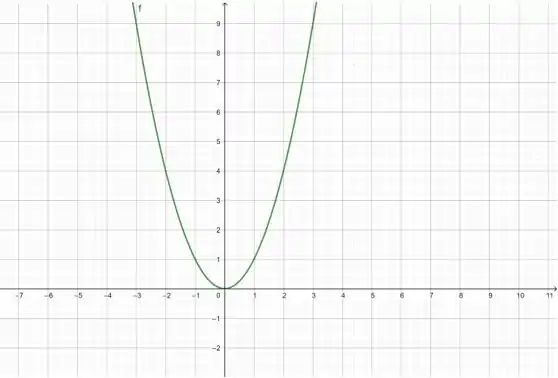
Olha como o vértice da parábola (a “bundinha” do gráfico) vai mudar de posição. Depois, :
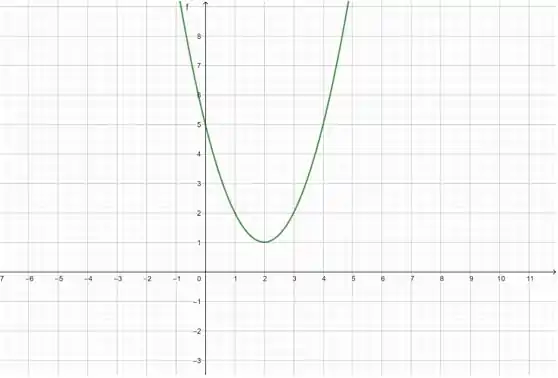
Repare que o gráfico realmente foi para a direita e para cima, em relação ao “antes”.
Resposta
Direita; 2; cima; 1.