Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.4 - Ex. 9
Determine uma janela retangular apropriada para a função dada e use-a para fazer o gráfico da função.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado nos pede para determinar uma janela retangular apropriada para a função dada e usá-la para fazer o gráfico da função:
Mas que janela é essa??
Então... quando a gente olha um gráfico, a gente quer tirar todas as informações que estão contidas nele. E, para isso, o gráfico não pode estar nem grande demais para o plano cartesiano e nem pequeno demais.
O tamanho ideal é aquele que contém o máximo de informações possíveis que podemos extrair do gráfico.
Para isso, precisamos calcular pontos chaves que nos dirão o tamanho correto da janela, isto é, descobrir pontos que nos forneçam informações suficientes sobre a função.
Nós sabemos que as funções trigonométricas têm um domínio definido para todo conjunto dos números reais. E que a função seno tem a imagem definida no intervalo:
Lembrando que a imagem são todos os valores de que a função pode assumir. Como a nossa função tá elevada ao quadrado, esse intervalo muda um pouco.
Além disso, uma outra informação importante para uma função trigonométrica é seu período, que é dado nesse caso por:
considerando uma função . Na nossa função, temos , certo?
Esse período nos diz a frequência de oscilações da função no gráfico. Então, quanto menor o período, maior será a frequência de oscilações e consequentemente o gráfico seria mais comprimido no eixo .
Essa informações já serão suficientes pra gente definir uma janela de visualização para o nosso gráfico.
Bora lá?? 😉
Passo 2
Nós vimos no passo anterior, que a imagem da função seno está sempre definida no intervalo de . Como nesse caso, nossa função está elevada ao quadrado, elevamos esse intervalo ao quadrado e teremos a imagem:
Além disso, nós vimos que para uma função , seu período é dado por . Como a nossa função, , tem
Seu período será:
Que é aproximadamente .
Como esse é um número bem pequeno, significa que nossa frequência de oscilações será bem alta em comparação com a função seno padrão (). Então, teremos um gráfico comprimido no eixo , pois haverá muitos ciclos de oscilação ocorrendo em um curto intervalo de .
Passo 3
Dessa forma, considerando que a nossa curva vai de até no eixo vertical e oscila em um intervalo tão pequeno, podemos considerar a janela:
Onde varia no intervalo e no intervalo e plotamos a curva :
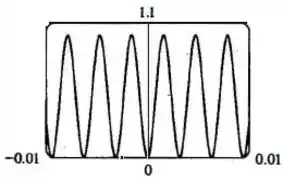
Assim, conseguimos visualizar e entender bem o comportamento periódico da função nesse intervalo.
Valeu, galera! Até a próxima! 😉