Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.4 - Ex. 8
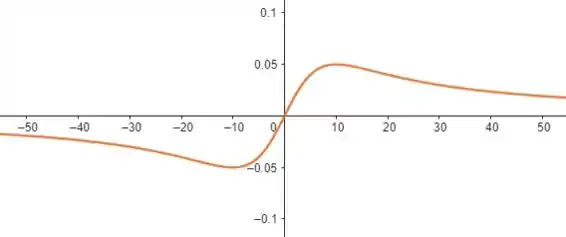
Determine uma janela retangular apropriada para a função dada e use-a para fazer o gráfico da função.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu a seguinte função:
A questão pede para fazermos um esboço do gráfico da função na janela apropriada.
Mas o que é uma janela retangular apropriada??
Bom... Uma janela retangular adequada para um gráfico é uma área no plano cartesiano que inclui todos os pontos relevantes da função sem cortá-la ou deixar partes dela de fora.
Ela deve ser dimensionada de forma a mostrar claramente o comportamento da função ao longo de um intervalo específico de valores de e .
Dessa forma, temos que analisar o intervalo de e em que a nossa função apresenta os pontos mais importantes, bem como analisar o comportamento dessa função.
Agora bora lá!! 😉
Passo 2
Vamos primeiro verificar se essa função é par ou ímpar (caso seja verdadeiro para qualquer uma das duas, só teremos que analisar um lado do eixo e duplicar a janela).
Fazendo , temos:
Trata-se de uma função ímpar!
Passo 3
Perceba que pelo denominador crescer de forma mais rápida que o numerador (por conta do ), tenderá a zero no infinito.
Assim, uma janela retangular que descreve bem o comportamento da nossa função é uma janela de tamanho :
