Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.5 - Ex. 21
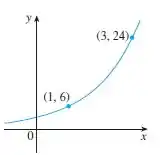
Encontre a função exponencial cujo gráfico é dado.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente encontrar a função exponencial cujo gráfico é dado por:
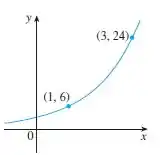
Olhando para o gráfico, vemos que a nossa função deve passar pelos pontos e . Então, vamos substituir esses pontos em para encontrar os valores de e e, assim, definir a nossa função de acordo com o gráfico.
Vamos lá!
Passo 2
Vamos começar substituindo o ponto na função:
Isolando , temos:
Vamos guardar esse resultado.
Passo 3
Agora, substituindo o ponto , vamos ter:
Substituindo a expressão de que encontramos no passo nessa equação, teremos:
Simplificando o com o :
Isolando :
E calculando a raiz em ambos os lados:
Ih, temos dois valores para ? É isso mesmo? Calma, como nós temos que o gráfico da função está crescendo, temos que . Logo, .
Passo 4
Com , de acordo com a relação que achamos no passo , temos que será:
Dessa forma, temos que nossa será:
Valeu, galera! Até a próxima! 😉