Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.4 - Ex. 20
Os gráficos se interceptam na janela retangular dada? Se eles se interceptarem, quantos pontos de interesecção existem?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado nos deu as funções e e quer saber se elas se interceptam na janela retangular por e em quantos pontos isso acontece.
Primeiro vamos entender o que isso tudo quer dizer.
Quando a gente plota um gráfico em um software ou calculadora gráfica, existe uma janela que limita a nossa visualização da imagem, expondo um recorte retangular da função. Essa janela, que é chamada aqui de janela retangular, diz respeito ao intervalo de variação de no eixo horizontal e de no eixo vertical. Então, de maneira geral, se tivermos uma janela retangular , teremos os intervalos:
Para o nosso caso, na janela , temos:
Então, é dentro desses intervalos que as nossas funções vão ser plotadas.
Nós temos uma reta e uma parábola e queremos saber se e onde elas se interceptam nessa janela, então vamos analisar o gráfico e encontrar os pontos onde essas curvas se tocam.
Vamos lá!
Passo 2
Plotando, com o axílio de um software, a parábola , de concavidade para baixo, e a reta na janela , vamos ter:
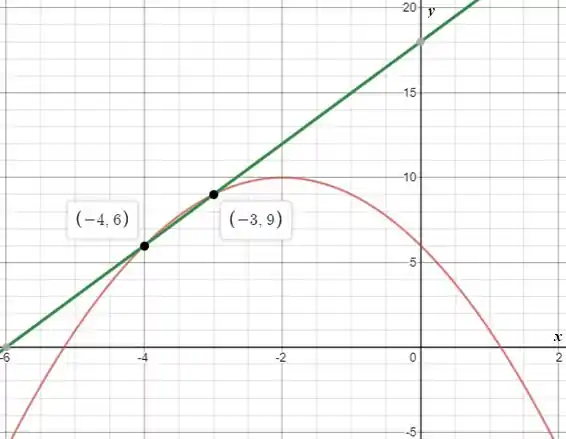
Observe que as curvas se encontram em dois pontos, em e em . Então, existem dois pontos de intececção.
E já encontramos a nossa resposta! Molezinha, né?
Valeu, galera! Até a próxima!