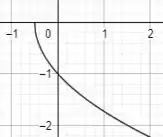
Faça o gráfico da função:
Comece pelo gráfico de uma das funções padrão apresentadas nas figuras 1.14-1.17 e aplique a mudança adequada.
Passo 1
Então galera, dentre as funções apresentadas na seção 1.1 do George, temos que a função que mais se encaixa é:
O gráfico dessa função é esse aqui:
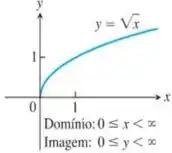
Pessoal, para podermos analisar essa função, teremos que manipula-la para tirar o 2 que está multiplicando a variável , tranquilo? Só assim conseguiremos analisar a partir da função supracitada.
Para tirarmos esse 2 de dentro da raíz, podemos fazer o seguinte:
Não tem problema fazermos isso porque estamos multiplicando e dividindo pelo mesmo valor, beleza?
Continuando o procedimento pra eliminar esse 2 de dentro da raíz, fazemos:
Passo 2
Opa! Agora sim conseguimos deixar a função mais bonitinha, não é? Feito isso, agora vamos analisar a função por partes. Vamos aos poucos inserindo as informações que nossa função original possui na função que mais se parece com ela, tranquilo?
Se pegarmos a função lá de cima que tomamos como referência, que é , e multiplicarmos ela por , o que vai acontecer é que o gráfico vai ser refletido em torno do eixo devido ao sinal negativo e alongado verticalmente por um fator , que no caso é .
Plotando então a função , temos:
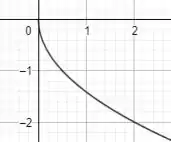
Passo 3
Por fim, para chegarmos na nossa função original basta que somemos juntinho de , não é mesmo? Sempre que somamos ou subtraímos um número diretamente na variável, o que acontece com o gráfico é que ele vai ser deslocado para a esquerda ou para a direita, tranquilo? Se for uma soma, vai ser deslocado para a esquerda. Se for uma subtração, vai ser deslocado para a direita.
Como no nosso caso é uma soma de meia unidade, então o gráfico vai ser deslocado de meia unidade para a esquerda. Se liga só como que o gráfico vai ficar:
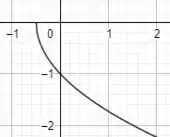
Resposta
O gráfico de é: