Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.2 - Ex. 55
A figura a seguir mostra o gráfico de uma função com domínio [0, 2] e imagem [0, 1]. Encontre os domínios e as imagens das funções a seguir e esboce os gráficos correspondentes.
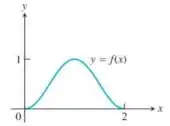
a)
b)
c)
d)
e)
f)
g)
g)
Passo 1
a) Pessoal, antes de resolvermos a letra a), vale ressaltar que para resolvermos todas essas questões devemos lembrar de algo muito importante! O domínio de uma função se trata dos valores de que a função pode assumir, já a imagem de uma função se trata dos valores de quando aplicamos um valor qualquer na função.
Parece um bixo de 7 cabeças, né? Relaxa, vamos ver que é mais tranquilo do que parece, olha só!
Quando há uma soma ou subtração na função, isso significa que a função vai ser deslocada verticalmente, sendo esse deslocamento para cima ou para baixo. Como temos uma soma de 2 unidades, então a função vai ser deslocada 2 unidades para cima.
O gráfico ficaria assim:
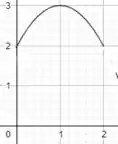
Domínio: [0,2]
Imagem: [2,3]
Passo 2
b) Utilizando literalmente o mesmo raciocínio da letra a), temos que o gráfico ficaria assim:
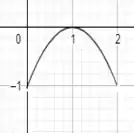
Domínio: [0,2]
Imagem: [-1,0]
Passo 3
c) Nessa função as coisas mudam um pouquinho, mas nada tão difícil também. Quando há um número multiplicando a função, como é o nosso caso, o que vai acontecer com a função é que ela vai ser alongada verticalmente por um fator , que nesse caso é 2. Sendo assim, o gráfico ficaria desse jeito ó:
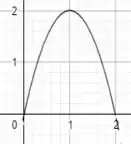
Domínio: [0,2]
Imagem: [0,2]
Passo 4
d) Esse caso parece ser a mesma coisa que o da questão anterior, não é? Então...
Quando o fator que foi comentado é -1, como é nesse caso, o que acontece com o gráfico é que a função vai ser refletida em torno do eixo . Se liga!
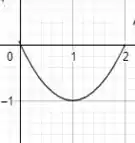
Domínio: [0,2]
Imagem: [-1,0]
Passo 5
e) Pessoal, nesse caso, quando há uma soma ou subtração diretamente na função, isso implica que a função vai ser deslocada horizontalmente. Tá, mas horizontalmente para a esquerda ou para a direita?
Se for uma soma, o deslocamento vai ser para a esquerda. Se for uma subtração, o deslocamento vai ser para a direita. Uma ou duas questões praticando isso e é garantia que você não vai mais esquecer!
Como no nosso caso se trata de uma soma de 2 unidades, então o gráfico vai se deslocar de 2 unidades para a esquerda, ficando assim:
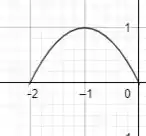
Domínio: [-2,0]
Imagem: [0,1]
Passo 6
f) Essa questão é a mesma coisa da questão anterior, pessoal! A diferença é que se trata de uma subtração, logo o deslocamento não será para a esquerda, será para a direita. Como há uma subtração de 1 unidade, então o gráfico vai ser deslocado 1 unidade para a direita, se liga:
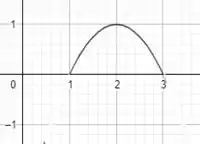
Domínio: [1,3]
Imagem: [0,1]
Passo 7
g) Essa questão é bem parecida com a da letra d), só que nesse caso a multiplicação acontece na variável e não na função . Na letra d) refletimos o gráfico em torno do eixo , nesse caso a reflexão acontece em torno do eixo . Dessa forma, o gráfico fica assim:
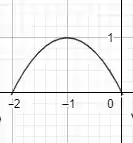
Domínio: [-2,0]
Imagem: [0,1]
Passo 8
h) Esse caso é um pouco mais elaborado porque envolve quase todos os tipos que vimos até aqui. Para facilitar, vamos por partes então:
Analisando apenas , sabemos que devido à soma de 1 unidade, a função vai ser deslocada 1 unidade para a esquerda. Além disso, assim como na questão d), como , então a função vai ser refletida em torno do eixo . Plotando essas informações ficaríamos com o seguinte gráfico:
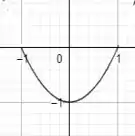
No entanto, ainda temos uma soma de 1 unidade nessa função. Como vimos nas questões a) e b), quando há uma soma ou subtração na função, isso significa que a função vai ser deslocada verticalmente. Nesse caso, como se trata de uma soma de 1 unidade, então a função vai ser deslocada 1 unidade para cima.
No fim das contas, o gráfico resultante é esse:
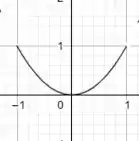
Domínio: [-1,1]
Imagem: [0,1]
Resposta
Ei, a resposta está no passo a passo :)