Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.2 - Ex. 45
Determine
E
- Calculando para valores de que tendem a 1 pela direita e pela esquerda
- Raciocinando como no exemplo 9
- A partir do gráfico de
Passo 1
Falaee, belezinha??
Bom... Aqui nos pedem para que resolvamos os seguintes limites laterais por diferentes estratégias:
E
Esses limites laterais representam o valor para o qual a função irá tender quando o se aproxima pela direita e pela esquerda.
Na letra a),vamos verificar esse valor substituindo o na função, com valores cada vez mais próximos de , sendo que para o limite pela esquerda vamos substituir valores que se aproximam de e que são menores que e pela direita vamos substituir valores que se aproximam de e que sãomaiores que .
Já na letra b), vamos raciocinar que essa função se trata de uma fração e a medida que substituímos o , o denominador do polinômio tende a zero, o que faz a fração ir para infinito. Só precisamos verificar se o denominador tende a zero por valores maiores que zero (positivos) ou menores que zero (negativos), pois isso nos dará um infinito positivo ou infinito negativo.
Por fim, na letra c), vamos fazer o gráfico dessa função e verificar o que acontece com ela quando tende a pela esquerda e pela direita.
Vamos ver em cada passo sobre cada uma delas, belezinha??
Passo 2
a) Iremos calcular os valores de para valores cada vez mais perto de 1, tanto para valores perto de 1 menores que 1 quanto para valores perto de 1 maiores de 1.
Faremos uma tabela para descobrir o valor dos limites, então
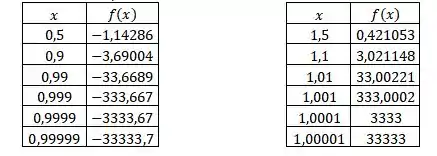
Pela análise da tabela, podemos ver que
E
Passo 3
b) Raciocinando como no Exemplo 9
Se é um pouco menor que 1, então é um valor que também é um pouco menor que , então será um número um pouco menor que e negativo e será um número negativo com grande valor absoluto. Então
Se é um pouco maior que 1, então é um pouco maior que e então será um número um pouco maior que e positivo e será um número positivo com grande valor absoluto. Então
Passo 4
c)
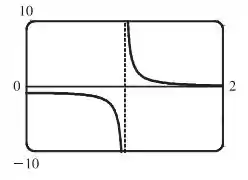
Pelo gráfico, podemos ver que quando se aproxima de pela esquerda, ou seja, pelos números menores, o limite tende a menos infinito. Portanto:
Por outro lado, podemos ver que quando se aproxima de pela direita, ou seja, pelos números maiores, o limite tende a mais infinito. Portanto:
Entendeu direitinho?? Responde aee 😉