Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.5 - Ex. 77
a) Se transladamos uma curva para a esquerda, o que acontece com sua reflexão em torno da reta ? Em vista deste princípio geométrico, encontre uma expressão para a inversa de
Em que é uma função injetora.
b) Encontre uma expressão para a inversa de
Em que .
Passo 1
Opaaa... tudo bem??
Nessa questão vamos analisar o que acontece com a reflexão de uma curva em torno da reta quando transladamos ela pra esquerda. Ou seja, queremos se vai ter algum comportamento padrão.
Pra isso, desenhamos numa tela a reta e uma curva... depois transladamos ela pra esquerda, que aqui é como se a gente girasse a curva em torno do eixo . A curva “sai” do papel girando pra esquerda e depois cai no papel de novo, mas acima da reta .
Ahhh... a curva é de uma função injetora... e, graficamente, pra função injetora a gente desenha uma curva que se passarmos várias retas horizontais, elas só vão cruzar a função uma vez. Esse é o gráfico de uma função injetora.
Depois de descobrir esse padrão vamos encontrar uma expressão para a inversa de:
E uma expressão para a inversa de:
Pra encontrar essas duas expressões vamos analisar apenas o gráfico e fazendo a manipulações na função .
Passo 2
Primeiro vamos desenhar num gráfico uma função injetora (em verde) abaixo da reta (em vermelho):
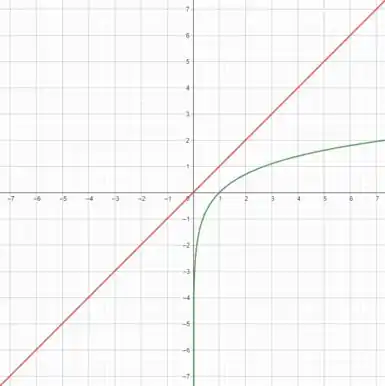
E se girarmos a curva em torno do eixo ela fica assim (curva roxa):
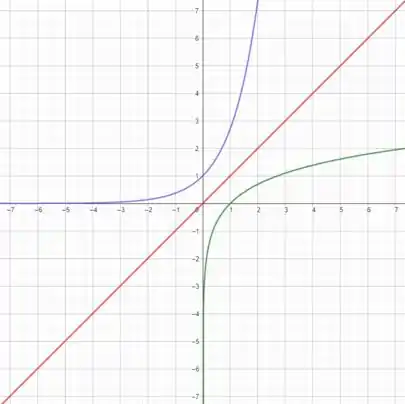
E nisso conseguimos ver que a curva fica espelhada em relação à reta . Essa é a característica gráfica da função inversa (espelhada em relação à ) .
Passo 3
Agora, pra achar uma função inversa de vamos mexer um pouco no gráfico. Como estamos adicionando uma constante ao , concorda que podemos só deslocar o gráfico de pra esquerda ou pra direita que aí já teríamos uma boa representação?
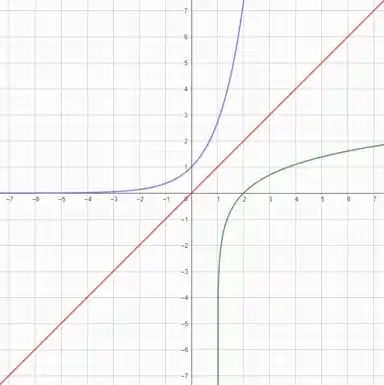
Mantivemos a reta vermelha, , e a curva roxa, que é a inversa , mas a curva verde chegou um pouco pro lado. Ela representa .
Agora precisamos deixar a cruva roxa de forma que ela vire o reflexo da curva verde. A gente só precisa subir ela um pouco, né? Que seria subir a curva roxa a mesma quantidade que a curva verde foi pra direita. Ficando assim:
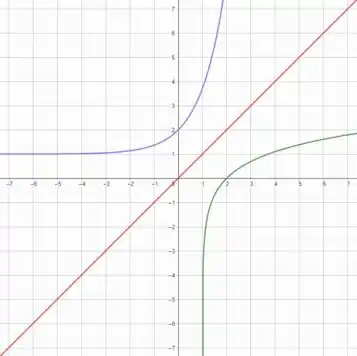
Pra deslocar uma função pra cima... adicionamos na parte do a quantidade que queremos deslocar. Maaaaaaas essa função que deslocamos pra cima é a função inversa. Qual o inverso de adicionar? Subtrair. Ficamos com:
Passo 4
Agora quermos a função inversa de Quando multiplicamos por alguma constante, o gráfico sobe um pouco:
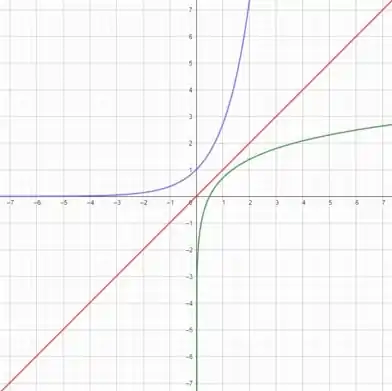
E pra fazer a curva roxa virar o reflexo da curva verda precisamos deslocar ela mais pra direita, né? Como pra função normal multiplicamos pela constante, então pra função inversa vamos dividir:
Resposta
a)
b)