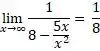Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.6 - Ex. 6a
Determine o limite da funçãoQUOTE _x0001_
Passo 1
Temos que calcular um limite no infinito, certo?
A ideia é se ligar que assim como nos outros cálculos de limites, podemos usar aquelas regras: do produto, da soma, do quociente e etc..
No nosso caso, como temos uma divisão, vamos usar primeiro a regra do quociente, então nossa conta vai ficar assim ó:
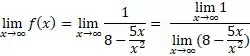
Passo 2
Olhando para o denominador da função do quociente lá de cima, temos uma subtração, então vamos usar a regra do subtração, véi:
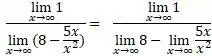
Passo 3
Agora é só substituir os resultados, mas antes temos que perceber umas coisinhas:
1ª coisa: Como QUOTE _x0001_
ele é uma constante e aí pela regra da constante,
Da mesma forma,
2ª coisa:
QUOTE _x0001_
Tá ligado no porque?
Isso acontece porque quando fazemos QUOTE _x0001_
, estamos fazendo uma divisão do 5 por valores cada vez maiores e então o resultado da divisão é cada vez menor. Por exemplo se tivéssemos 5 reais para dividir entre 2 pessoas, o valor seria razoável, mas e se fosse pra 100? Para mil? Percebeu?
Passo 4
Então agora é só substituir os valores:
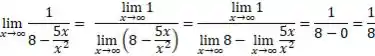
Resposta
