Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.2 - Ex. 37
Determine o limite infinito.
Passo 1
Eaeee, belezinha?? Bom... o enunciado nos dá o seguinte limite:
Ainda de acordo com o enunciado, o resultado desse limite é um número que tende ao infinito.
Mas qual infinito? Positivo ou negativo??
Para descobrirmos isso, teremos que estudar bem o nosso limite.
Como assim??
Bom... basicamente vamos ver o que acontece com o sinal do numerador e do denominador quando (quando tende a pelos números maiores que ele).
Com os sinais de cada um, podemos definir o sinal geral do nosso limite!!
Ah, a gente pode fazer isso por conta da seguinte propriedade:
Agora bora lá!! 😉
Passo 2
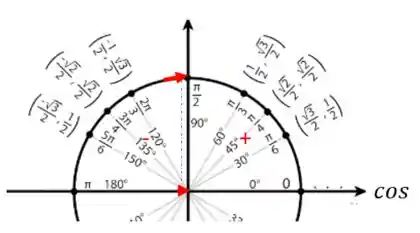
Analisando primeiramente o numerador:
Sabemos que a secante é o inverso do cosseno, ou seja:
Perceba que quando , o cosseno tende a zero pelo lado negativo da seguinte forma:
Passo 3
Agora, analisando o denominador, temos:
Perceba que nosso limite tende a um número positivo e próximo de !!
Passo 4
Dessa forma, temos uma divisão de um número negativo por um positivo.
E uma divisão entre um número negativo e um positivo resulta em um número negativo, ou seja:
Passo 5
Podemos observar esse comportamento pelo gráfico de :
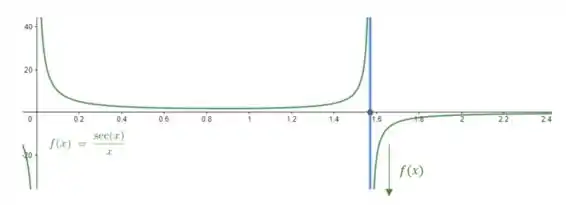
Perceba que quando (em azul), a função (em verde) tende a .