Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 3.1 - Ex. 62
Onde a linha normal da parábola no ponto cruza a parábola uma segunda vez? Ilustre com um esboço.
Passo 1
Bom galera, o problema quer saber se uma linha normal que passe pelo ponto da curva passa por algum outro ponto, para isso vamos encontrar a equação dessa linha normal.
A equação da linha é dada por:
E é o coeficiente angular da linha, e a gente pode encontrar por essa relação com a derivada:
Passo 2
Beleza, a gente quer encontrar o coeficiente angular, para isso vamos usar a relação com a derivada para o que é o ponto de intersseção:
A gente deriva a função da curva rapidindo com a regra geral e da soma:
Vamos usar a relação e fica:
Então:
Passo 3
Show de bola, a gente a gente já tem o ponto:
E o coeficiente angular:
Então vamos usar a equação da reta com o que já temos para encontrar o que falta:
Assim encontramos:
Passo 4
Continuando, nós só precisamos montar as equações com o que a gente encontrou:
A gente iguala essa equação com a da curva pra encontrar-mos as interseções:
Resolvendo:
Encontramos e . Como já usamos o , vamos calcular o ponto em :
Passo 5
Logo, o segundo ponto de interseção é . Fazendo um gráfico fica assim:
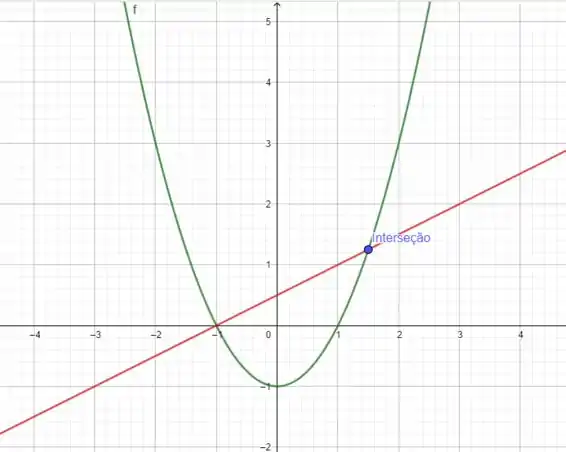
Resposta
Sim, no ponto .