Determine o limite infinito.
Passo 1
E aí! tudo certinho? 😊

Nesse problema queremos mostrar que o limite tende ao infinito.
Tem ideia de como fazer isso? 😬
Bom, o limite de uma função em um ponto é o valor que a função se aproxima à medida que a variável independente se aproxima desse ponto, sem necessariamente alcançá-lo. No entanto, em certos casos, é crucial considerar as abordagens da esquerda e da direita separadamente. Isso é onde os limites laterais entram em jogo.
Considere uma função e um ponto no domínio de . O limite lateral esquerdo de quando se aproxima de é denotado por . Isso significa que estamos observando o comportamento de à medida que se aproxima de a partir de valores menores que Em outras palavras, estamos examinando o que acontece com a função à esquerda de
Da mesma forma, o limite lateral direito de quando se aproxima de é denotado por . Isso implica que estamos analisando o comportamento de à medida que se aproxima de a partir de valores maiores que ou seja, à direita de
Passo 2
Se ambos os limites laterais se aproximam de um mesmo valor à medida que se aproxima de então o limite da função quando se aproxima de existe e é igual a Isso é representado por:
No entanto, se os limites laterais esquerdo e direito de não convergirem para o mesmo valor conforme se aproxima de então o limite de quando se aproxima de não existe.
Em resumo, os limites laterais permitem examinar o comportamento de uma função em torno de um ponto específico, distinguindo entre as abordagens à esquerda e à direita desse ponto.
Isso é essencial para compreender melhor as características das funções, como descontinuidades, assíntotas e outros comportamentos singulares.
Passo 3
Quando se trata de limite, temos que analisar os valores que as funções tendem a assumir quando a variável se aproxima de um determinado valor.
Então temos que ter em mente que não estamos buscando o valor exato, estamos buscando o valor que a função tende a assumir.
Veja só! 😉
Dado o limite:
Para resolver isso, primeiro vamos analisar cada termo individualmente quando se aproxima de 0.
Passo 4
Para
Quando se aproxima de 0, também se aproxima de 0.
Nesse caso, a função está avaliando o logaritmo natural de números que se aproximam de zero.
Lembre-se de que para próximo a , será um número muito pequeno e positivo.
Assim, estará avaliando o logaritmo de um número positivo próximo de zero, o que resulta em um valor tendendo a , pois o logaritmo natural de um número entre é negativo.
Passo 5
Para
Conforme se aproxima de , se aproxima de , pois , e quando se aproxima de , o denominador se aproxima de , tornando o valor do termo cada vez maior e positivo.
Agora, ao calcular o limite da função original, estamos essencialmente subtraindo um valor tendendo a de um valor tendendo a :
Quando você subtrai um número infinitamente grande de um número infinitamente pequeno, o resultado é um número que tende para , pois a contribuição negativa é maior do que a contribuição positiva.
Portanto, o limite infinito da função original é
Tranquilo até aqui? 😉
Passo 6
Comprovando graficamente nosso resultado
Um limite convergente é uma propriedade fundamental de uma função que descreve o comportamento da função à medida que a variável independente se aproxima de um determinado valor.
Em termos simples, quando dizemos que o limite de uma função é convergente, estamos afirmando que, à medida que a variável independente se aproxima de um determinado valor, a função se aproxima de um valor específico.
Portanto, um limite convergente descreve a tendência de uma função à medida que sua variável independente se aproxima de um determinado valor, como mostra o gráfico a seguir
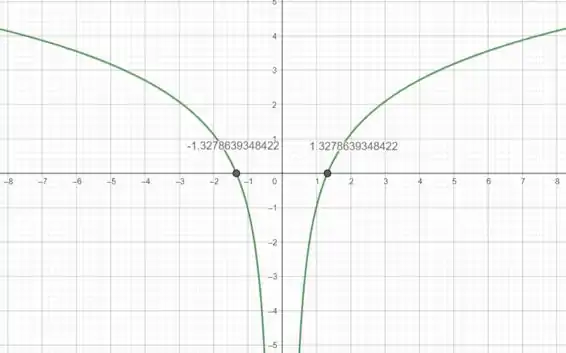
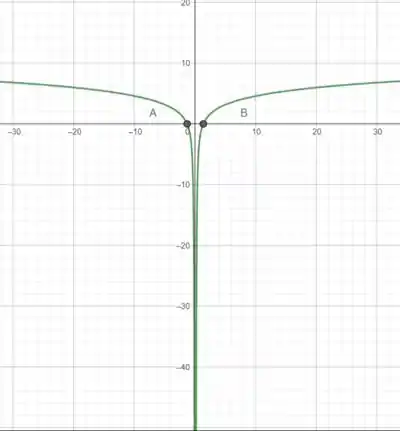
Podemos assim então, confirmar o que foi encontrado no passo 2:
O que achou? Entendeu tudo? Responde Aí! 😁