Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.2 - Ex. 32
Determine o limite infinito.
Passo 1
Olá, meu parceiro. Vamos resolver hoje mais uma atividade.
Aqui iremos determinar o limite infinito:
Os limites infinitos ocorrem muitas vezes quando temos situações de limites laterais, onde nos aproximamos de um valor ou pela esquerda ou pela direita. Mas lembre-se que nessas situações estamos infinitesimalmente próximos do valor, mas não de fato no valor, isso faz com que em situações de divisão, termos uma divisão de um valor qualquer diferente de zero por um número infinitesimalmente pequenos, fazendo com que tenhamos uma ‘explosão’ do limite ao infinito.
O limite em si não existe, pois, infinito não é um número, é um indicativo que nossa função caminha indefinidamente para valores absurdamente grandes.
Passo 2
Agora vamos para a resolução:
Aqui então, temos valores infinitesimalmente menores que 5, sendo assim iremos explodir para valores negativos.
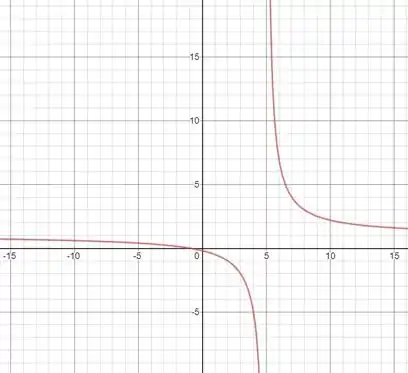
Podemos confirmar o valor obtido através da análise do gráfico da função:
