Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.2 - Ex. 40
Determine o limite infinito.
Passo 1
Eaee, belezinha?? Bom... queremos determinar o seguinte limite infinito:
Bom... a gente sabe que esse limite vai resultar no infinito. Mas qual infinito? Positivo ou negativo?
Perceba que tende a pelos valores à esquerda de (por isso que tem um escrito como expoente). Trata-se do limite lateral à esquerda de .
Para verificarmos o resultado desse limite, vamos ter que fazer algumas simplificações e utilizar essa análise de limite lateral.
Em outras palavras, depois de simplificarmos a expressão dentro do limite, temos que nos perguntar:
“O que acontece quando esse chega beeeem perto de pela esquerda??”
Bora junto aqui!!! 😉
Passo 2
Analisaremos o limite de:
Podemos reescrever esse limite como:
Passo 3
Agora vamos colocar um número bem próximo de pela esquerda para podermos enxergar melhor:
Perceba duas coisas:
- O numerador é um número positivo;
- e o resultado do denominador será um número negativo.
Dessa forma, a divisão de um número positivo por outro negativo vai resultar em um número negativo!!!
Portanto, podemos concluir que:
Passo 4
Analisando parte do gráfico da função:
No ponto de interesse, temos:
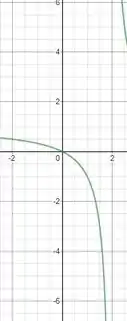
Podemos então, confirmar o que foi encontrado no passo 3: