Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.2 - Ex. 31
Determine o limite infinito:
Passo 1
Fala povo, tudo certo? Seguinte... queremos calcular o seguinte limite:
Pra achar esse limite, uma coisa que podemos fazer é usar as propriedades dos limites e escrever:
Agora vamos verificar cada um dos limites!! 😉
Passo 2
Agora, resolvendo o limite de cima, temos:
Ou seja:
O próprio enunciado diz pra gente que esse limite dá infinito, mas qual deles? ou ? Bora descobrir!!
Passo 3
Bem, o resultado do limite vai depender só do denominador, ok? Ele era:
Agora, nota bem a função dentro desse limite:
Não parece muito com uma função tal que:
Que é uma parábola com concavidade pra cima.
Isso porque é bem parecido mesmo, nada mais é do que deslocado uma unidade pra direita:
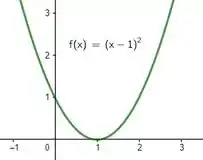
Hmm... então não importa pra qual lado eu tenda de , direita ou esquerda, das duas formas esse resultado vai dar:
Passo 4
Juntando os dois resultados então:
Um número positivo () dividido por um número infinitamente próximo de zero e também positivo vai dar um número infinitamente grande e bem, positivo hahaha. 😉