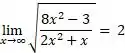Determine o limite QUOTE _x0001_![]()
Passo 1
Nosso objetivo é encontrar um número que representa o limite, desde ele exista, certo? Então temos que se ligar que assim como nos outros cálculos de limites, podemos usar aquelas regras do produto, da soma, do quociente e etc...
Como no limite que devemos calcular tem uma raiz ai na frente, então você vai passar com o limite pra dentro da raiz. Isso mesmo! Olhando a raiz como uma função, temos que ela é contínua, então o limite pode dá aquela puladinha, beleza?
Ou seja, nossa contas ficam:
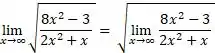
Passo 2
Agora, veja que estamos com uma divisão de polinômios e, quando QUOTE _x0001_![]() .
.
Daí,
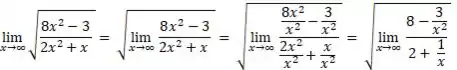
Passo 3
Usando a regra do quociente: “O limite do quociente é o quociente dos limites”, temos
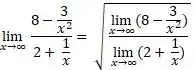
Passo 4
Pela regra da soma e da subtração: “ O limite da soma é a soma dos limites” e “o limite da subtração é a subtração dos limites”, nossa conta fica:
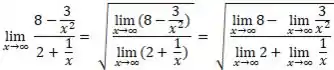
Passo 5
Para prosseguir, precisamos lembrar de mais algumas coisas:
1ª coisa: Como 8 não depende de QUOTE _x0001_![]() ele é uma constante e aí pela regra da constante,
ele é uma constante e aí pela regra da constante,
QUOTE _x0001_![]()
Da mesma forma,
QUOTE _x0001_![]()
2ª coisa:
QUOTE _x0001_![]()
Vou tentar ilustrar rapidinho:
Imagine que você tem R$100,00 para dividir para nós dxs, beleza ? Então, a quantidade que vamos receber seria R$50,00 Mas e se agora você tiver que dividir para cem pessoas, o valor vai ser bem menor, não é ? Mas e se for para mil pessoas? Menor ainda, concorda comigo, migxs? Então, o valor recebido por cada um de nós é cada vez menor à medida que aumentamos a quantidade de pessoas que temos que dividir o money, ou seja, estamos ficando com quase nada, né?!! O valor a receber por nós tende a zero.
Tá, se olharmos para esse R$100,00 como nosso QUOTE _x0001_![]() tender a infinito é como se estivessemos dividindo o 3 por valores cada vez maiores, consequentemente
tender a infinito é como se estivessemos dividindo o 3 por valores cada vez maiores, consequentemente
![]()
Da mesma forma,
![]()
Passo 6
Então, substituindo naquela bagaça
QUOTE _x0001_
Logo,
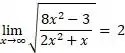
Resposta