Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.11 - Ex. 53
Estime o volume do material presente em uma embalagem cilíndrica de 30 polegadas de altura, 6 polegadas de raio e 0,5 polegada de espessura.
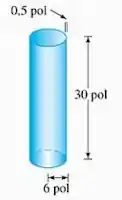
Passo 1
Bom, o volume do material vai depender da espessura que é como se fosse a variação do raio, nesse caso.
Sabemos que o volume do cilindro é dado por: .
Assim, a variação do volume que é dado pela derivada, sendo a altura fixa é:
Passo 2
Temos pelo enunciado que: ,
Assim, substituindo os valores na fórmula anterior, temos:
Resposta
O volume estimado de material da embalagem é .
Exercícios de Livros Relacionados
Quão exata deve ser a medição do diâmetro interno de um tanque cilíndrico de armazenagem com 10 m de altura para que o cálculo de seu volume fique a 1 % do valor real? Quão exata deve ser a medição do
O diâmetro de uma esfera é medido como 100 ± 1 cm e o volume é calculado a partir dessa medição. Estime a porcentagem de erro no cálculo do volume.
A altura e o raio de um cilindro circular reto são iguais, de modo que o volume desse cilindro é dado por V = π h 3 O volume deve ser calculado com um erro menor que 1% em relação ao valor real. Deter
O diâmetro de uma árvore era de 10 polegadas. No ano seguinte, a circunferência aumentou 2 polegadas. Qual foi a variação aproximada do diâmetro da árvore? E da área da seção transversal?