Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 7.3 - Ex. 85
Mostre que a área da região no primeiro quadrante circundada pela curva , os eixos coordenados e a reta é a mesma que a área de um retângulo de altura e comprimento s, onde s é o comprimento da curva de até . Ilustre esse resultado com uma figura.
Passo 1
Para encontrar o comprimento da curva, usamos a fórmula do comprimento:
Temos que então, substituímos, lembrando que só estamos considerando valores do primeiro quadrante...
Usando a identidade trigonométrica , ficamos com:
Então a área do retângulo de altura e comprimento é dada por:
Passo 2
Vamos para a área da função agora. A área sobre a curva é dada por:
Então, , ou seja, a área sobre a curva é igual a área do retângulo com altura igual a e comprimento igual a , como queríamos mostrar.
Passo 3
A ilustração desse resultado pode ser visto no gráfico a seguir:
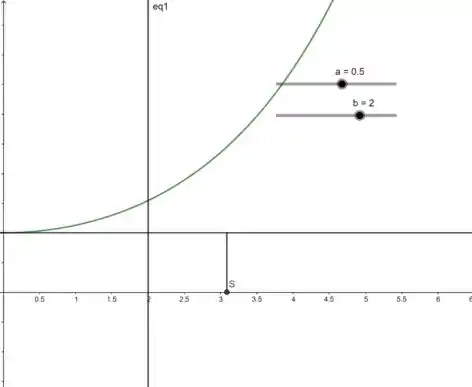
Resposta
Ei, a resposta está no passo a passo :)