Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 13.2 - Ex. 30
(a) Determine o ponto de interseção das retas tangente à curva
No ponto e .
(b) Ilustre traçando o gráfico da curva e ambas as tangentes.
Passo 1
Olá, meu esforçado estudante. Vou te ajudar a resolver essa atividade e você vai sair daqui dando aula.
A gente quer aqui, primeiro encontrar o ponto de interseção das retas que são tangentes a curva:
No ponto e .
E depois iremos ilustrar a situação.
Para determinar o ponto no qual as duas retas tangentes se cruzam precisamos encontrar a equação paramétrica de ambas as retas, para isso vamos precisar de um ponto e um vetor pertencente a cada reta.
Tendo as duas equações basta igualarmos elas e encontrar o parâmetro que corresponde justamente ao ponto no qual elas se cruzam. Com esse parâmetro em mãos basta substituir em qualquer uma das equações das retas que encontramos o ponto de interseção.
Passo 2
- O vetor da reta tangente pode ser encontrado a partir da derivada da curva aplicada no ponto referente a um dos parâmetros.
O parâmetro corresponde ao ponto:
Temos então que o ponto é:
O parâmetro corresponde ao ponto:
Ficamos então com:
A derivada de é encontrado utilizando da regra da cadeia e das derivadas trigonométricas que são tabeladas:
Aplicada em e :
Então a equação paramétrica das retas tangentes são:
E
Onde são os pontos pelo quais nossa função passa, e vem da derivada. Então a gente tem que nossas retas parametrizadas são:
Para :
Para :
Igualando as duas equações encontramos que o parâmetro do ponto de interseção é:
Substituindo esse parâmetro na equação de qualquer uma das retas tangentes obtemos que o ponto associado a ele é , onde este é o ponto de interseção.
Passo 3
b) O gráfico da curva juntamente com as retas tangentes a gente vai obter utilizando o GeoGebra 3D:
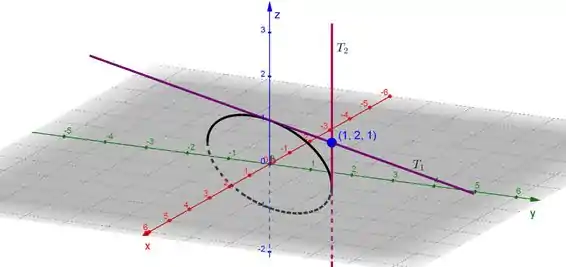
Resposta
a) Ponto de interseção: .