Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 13.1 - Ex. 7

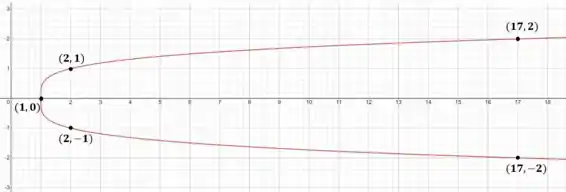
Esboce o gráfico da curva cuja equação vetorial é dada. Identifique com seta a direção na qual o parâmetro cresce

Passo 1

Fala ai pessoal! Tudo tranquilo?

Bora para mais um questãozinha. O que vamos fazer aqui?

Nesta questão vamos plotar o gráfico da equação vetorial , mas para isso temos primeiro que supor valores para pois assim, teremos o valor de e .

Vamos enterder um poudo mais. Bora!

Passo 2

A equação é uma equação vetorial, logo ele é composto pelas componentes que correspondem respectivamente aos eixos .

Uma das técnicas para plotar o gráfico desta equação vetorial é ir supondo valores de e verificar quanto vale o ponto .

Logo,

Vamos fazer uma tabela para nos auxiliar:

Passo 3

Agora para construirmos o gráfico, temos que pegar os pontos de e .

Por exemplo, os pontos , , , e

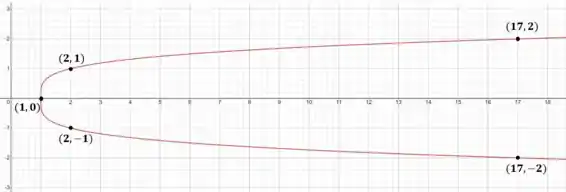
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o comprimento da curva com precisão de quatro casas decimais.(Use sua calculadora para aproximar a integral.) r t = t ,t ,t 2 , 1 ≤ t ≤ 4

Encontre o comprimento da curva com precisão de quatro casas decimais.(Use sua calculadora para aproximar a integral.) r t = s e nt , cos ⁡ t ,t gt , 0 ≤ t ≤ π / 4

Reparametrize a curva com relação ao comprimento de arco medido a partir do ponto onde t = 0 na direção crescente de t . r t = 2 ti + 1 - 3 t j + 5 + 4 t k

Suponha que você comece no ponto (0, 0, 3) e se mova 5 unidades ao longo da curva x = 3 s e n t , y = 4 t , z = 3 cos ⁡ t na direção positiva. Onde você está agora?

Trace a curva com equações paramétricas x = s e nt , y = s e n2 t , z = s e n3 t . Encontre o comprimento total desta curva com precisão de quatro casas decimais.