Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 13.1 - Ex. 28
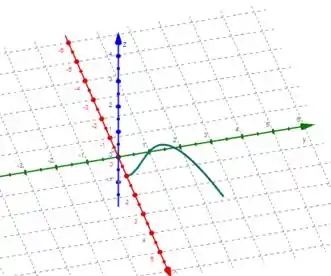
Utilize um computador para traçar a curva da equação vetorial dada. Escolha o domínio do parâmetro e ponto de vista de forma a revelar a verdadeira natureza da curva.
Passo 1
Eaee, belezinha?? Bom... O enunciado nos deu a seguinte função vetorial:
Queremos plotar a sua curva e, para isso, precisaremos utilizar um software matemático.
Além disso, queremos escolher bem o domínio do parâmetro e ponto de vista de forma a revelar a verdadeira natureza da curva.
Agora bora lá!! 😉
Passo 2
Essa curva está parametrizada pelo parâmetro , para traçar ela precisamos escolher um domínio para esse parâmetro e aqui podemos escolher todos os números reais que não terá nenhum problema, devido ao fato de suas componentes serem contínuas, portanto:
No ponto de vista “superior”, ou seja, no plano , teríamos uma função do quarto grau, e no plano teríamos uma parábola voltada pra cima.
Para termos uma visualização real da curva parametrizada dada, é necessário uma visão ampla, abrangendo os planos coordenados simultaneamente, veja:
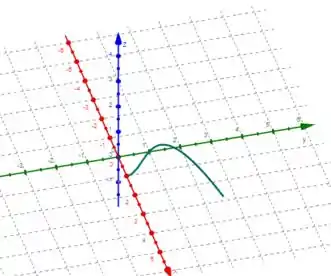
Esse é o melhor ângulo que podemos enxergar a figura 😉.
Aah... só lembrando que ela está no lado positivo de cada uma das coordenadas. Veja outras perspectivas dela ao rotacionar o eixo no sentido horário:
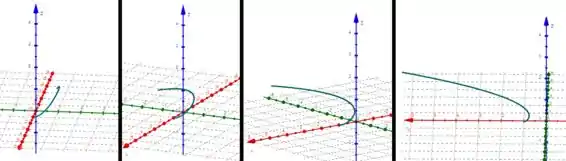
Resposta
