Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 12.2 - Ex. 15
Determine a soma dos vetores dados e ilustre geometricamente.
13.
Passo 1
Queremos determinar a soma dos vetores dados. Bom, para somar dois vetores, basta somarmos suas coordenadas componente a componente, assim:
Passo 2
Agora precisamos desenhar nossa soma:
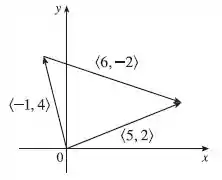
Resposta
13.
Exercícios de Livros Relacionados
Os lados do triângulo equilátero A B C têm medida 2. Calcule A B → ⋅ B C → + B C → ⋅ C A → + C A → ⋅ A B → .
São dadas as bases ortonormais E e F . Determine a e b , sabendo que u → = 1 ,1 ,2 E = b ,a ,1 F e v → = 1 ,2 ,3 E = 3 ,1 ,2 F .
São dadas as coordenadas de u → e v → em relação a uma base ortonormal fixada. Calcule, em radianos, a medida angular entre u → e v → . u → = 1 ,0 ,1 e v → = ( - 2 ,10 ,2 )
Sejam B = i → ,j → ,k → uma base ortonormal, u → = x ,y ,z B ≠ 0 → , α = a n gu → ,i → , β = a n g( u → ,j → ) e γ = a n gu → ,k → . Cada um dos números cos α , cos β , cos γ chama-se cosseno di
São dadas as coordenadas de u → e v → em relação a uma base ortonormal fixada. Calcule, em radianos, a medida angular entre u → e v → . u → = - 1 ,1 ,1 e v → = ( 1 ,1 ,1 )