Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.9 - Ex. 53
Determine de tal forma que a região acima da curva à direita do eixo e abaixo da reta tenha uma área de unidades quadradas, onde .
Passo 1
Vamos lá! A primeira coisa a se fazer é desenhar a curva e a reta que o problema deu.
Temos a curva que é justamente uma parábola com vértice na origem e concavidade para cima pois o coeficiente do é .
Também temos a reta com e isso nos dá uma reta horizontal acima do eixo . Podemos então esboçar isso tudo em um plano cartesiano.
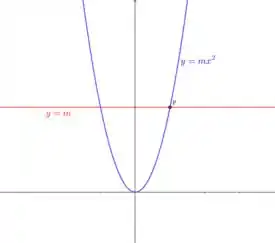
Como vocês podem observar, vamos ter uma região acima da parábola e abaixo da reta, a questão pediu para determinar de tal forma que a região à direita do eixo (região verde) seja unidades quadradas.
Passo 2
Agora nós vamos utilizar a integral definida para representar a região pedida, a princípio faremos a integral da função maior menos a menor, ou seja, e com o intervalo de integração para pegar a área entre as curvas.
Percebam que o limite superior é a abscissa do ponto de interseção entre a reta e a parábola. Vejamos que ponto é esse então da seguinte forma:
Daí temos que , ou , o único valor possível é pois estamos à direita do eixo e . Dessa forma, a área é dada por:
Passo 3
Para resolver a integral, vamos utilizar:
Sabemos da integral definida que:
Em que é uma primitiva de . Diante disso, ficamos com:
Passo 4
Bom, achamos a área entre as curvas da região pedida, mas a questão quer saber qual valor de torna essa área igual a . Então façamos o seguinte: