Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.9 - Ex. 54
Se unidades quadradas for a área da região limitada pela parábola e pela reta , acha a taxa de variação de em relação a .
Passo 1
Vamos lá! Antes de pensar em calcular a taxa de variação da área e tals, precisamos saber a área, né? Então a primeira coisa a se fazer é achar a área e para isso vamos desenhar a curva e a reta que o problema deu. Vamos desenhar a reta de tal forma que tenha interseção com a primeira curva.
Temos a curva que é justamente uma parábola com vértice na origem e concavidade para direita, perceba que aqui temos algo como e esse .
Também temos a reta com e isso nos dá uma reta que passa na origem e tem coeficiente angular positivo, ou seja, uma reta crescente. Podemos então esboçar isso tudo em um plano cartesiano.
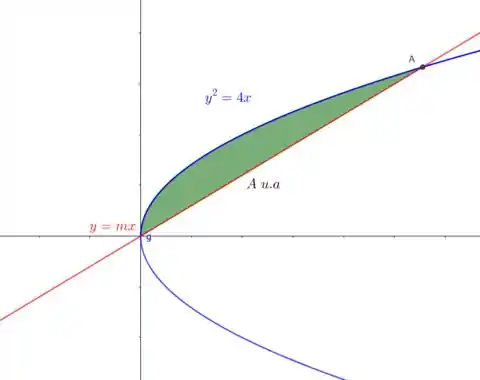
Como vocês podem observar, vamos ter uma região abaixo da parábola e acima da reta, perceba também que só vamos estar interessados no primeiro quadrante, pois a reta é crescente.
Passo 2
Agora nós vamos utilizar a integral definida para representar a região pedida, a princípio faremos a integral da função maior menos a menor, ou seja, e com o intervalo de integração para pegar a área entre as curvas. Mas quem é ? É a função que nos dá o ramo da parábola do primeiro quadrante. Vamos achar:
Sendo assim, a área é dada por:
Percebam que o limite superior é a abscissa do ponto de interseção entre a reta e o ramo da parábola. Vamos achar esse ponto então:
Daí temos que ou , o único valor possível é pois nos daria a origem. Dessa forma, a área é dada por:
Passo 3
Agora nós já podemos achar a taxa de variação da área em relação a . Podemos fazer isso derivando diretamente a integral em relação a ou resolvendo essa integral definida e derivar o resultado, que nada mais é do que a área também. Vamos derivar diretamente a integral usando a fórmula do teorema fundamental do cálculo:
Ficamos então com:
Na integral em que temos multiplicando, tivemos que utilizar a regra do produto da derivada. Sendo assim,
Aqui vamos usar .
Dessa forma,
Sendo assim a taxa de variação da área em relação a é .