Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.1 - Ex. 36
Encontre uma reta vertical que divida a área englobada pelas curvas , e em duas partes iguais.
Passo 1
Para encontrar a região englobada por curvas, precisamos analisar a região dada e montar a integral:
Ou
E calculá-la.
O pulo do gato aqui é perceber que se divide a área da região acima do eixo entre e ao meio, então a área entre e e a área entre (acima do eixo ) são iguais. O que precisamos fazer é calcular essas duas integrais e igualá-las para descobrir . Vamos lá!
Passo 2
Essas são as duas regiões que temos:
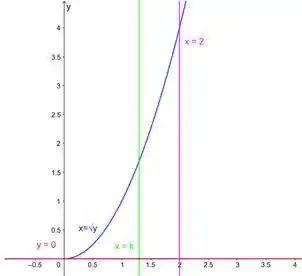
Para facilitar nossa vida, podemos usar em vez de , e fazer a integral em relação a , porque nossos extremos de integração podem ser tirados diretamente do gráfico. Belezinha?
A região do lado direito de vamos chamar de . Ela está limitada por cima pela parábola e por baixo pela reta . Os extremos de integração são e . Ela fica com essa carinha:
A área do lado esquerdo da reta é bem parecida, só temos mudanças nos extremos de integração:
Passo 3
Agora igualamos as duas áreas e calculamos as integrais para descobrir quem é :
Isolando :