Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.1 - Ex. 38
Encontre a região englobada pela curva e a reta que passa pelos pontos e na curva.
Passo 1
Para encontrar a região englobada por curvas, precisamos analisar a região dada e montar a integral:
Ou
E calculá-la.
O charme desse exercício é só que a gente precisa achar a expressão de uma dessas funções. Mas vai ser tranquilo.
Vamos lá!
Passo 2
Essa é a nossa região:
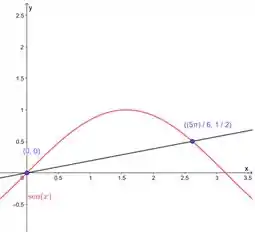
Vemos que ela está limitada superiormente pelo seno e inferiormente pela reta, duas funções de , logo integramos em . Mas quem é essa reta?
Como ela passa pela origem, só precisamos calcular seu coeficiente angular:
Os extremos de integração podemos ver pela coordenada dos pontos dados:
Nossa integral fica assim:
Passo 3
Agora é só calcular:
Resposta
Exercícios de Livros Relacionados
Esboce a região delimitada pelas curvas indicadas e encontre sua área. x = y 4 , y = 2 - x , y = 0
Esboce a região delimitada pelas curvas indicadas e encontre sua área. y = cos π x , y = 4 x 2 - 1
Represente graficamente a região entre as curvas e use a calculadora para encontrar a área correta até a quinta casa decimal. y = e 1 - x 2 ,y = x 4
Represente graficamente a região entre as curvas e use a calculadora para encontrar a área correta até a quinta casa decimal. y = tan 2 x ,y = x
Esboce a região delimitada pelas curvas indicadas e encontre sua área. y = cos x , y = sin 2 x , x = 0 ,x = π 2