Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.3 - Ex. 58

Determine a tangente à (curva) bruxa de Agnesi (representada a seguir) no ponto 2,1 .

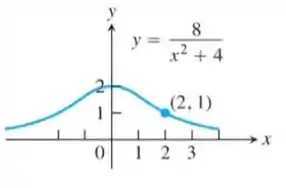
Passo 1

A primeira coisa que precisamos lembrar é que quando é pedido a tangente de uma curva, precisamos primeiro achar o coeficiente angular da tangente (derivada da curva). Então para isso, vamos encontrar a derivada da curva

y ' = 8 x 2 + 4 '

y ' = 8 ' x 2 + 4 - 8 x 2 + 4 ' x 2 + 4 2

y ' = 0 ∙ x 2 + 4 - 8 2 x 2 - 1 + 0 x 2 + 4 2

y ' = - 8 ∙ 2 x x 2 + 4 2

y ' = - 16 x x 2 + 4 2

Passo 2

Em seguida, vamos substituir os valores de x em y '

y ' = - 16 x x 2 + 4 2

y ' 2 = - 16 ∙ 2 2 2 + 4 2 = - 32 8 2 = - 32 64 = - 1 2

Passo 3

Agora que encontramos os coeficientes angulares, vamos substituir na equação da tangente:

y - f a = f ' a x - a

y - 1 = - 1 2 x - 2

y - 1 = - x 2 + 1

y = - x 2 + 2

Prontinho!!!

Resposta

y = - x 2 + 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

54. Se f e g são duas funções, tais que suas derivadas primeira e segunda existem e h é uma função definida pela equação hx =f x ⋅ g ( x ) , prove que h ' ' ( x ) = f x ⋅ g ' ' x+2 f ' x g ' x +f ' '
56. Se y = 1 1 - 2 x Prove, por indução matemática, que d n y d x n = 2 n n ! 1 - 2 x n + 1
58. Obtenha uma fórmula similar a do Exercício 57 para D x n ( c o s x ) .
51. Para a função do Exercício 49, ache f ' ' ' ( x ) quando ela existir.
52. Mostre que sex y = 1 , então d ² y d x ² ⋅ d 2 x d y 2 = 4 . ² ²