Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.6 - Ex. 65b
Determine o valor exato da expressão:
Passo 1
E aí, galera! Seguinte: eu sei que esse “” assusta, mas saiba duas coisas:
- Isso não é a mesma coisa que !!
- Então o que é? É a mesma coisa que . O que é isso? É o arco que tem determinado valor para seno
Calma, que vai ficar mais claro pra você daqui a pouco. Mas antes, preciso que você tenha em mente os arcos fundamentais e seus senos e cossenos correspondentes, ok?
Por exemplo:
30° () e
45°()
60°() e
Vamos lembrar outra coisa também:
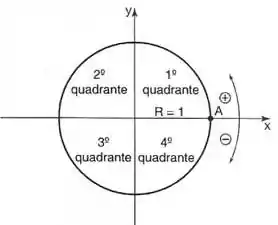
Saca só esse Círculo Trigonométrico! Tá vendo que, quando você pega um ângulo no sentido anti-horário, o sinal do ângulo é positivo e, quando pega um ângulo no sentido horário, o sinal dele é negativo? Isso é importante. Se você tem dúvidas nessa matéria, sugiro você fazer uma revisãozinha, porque esse conceito é importante.
Outra coisa: o seno de um ângulo negativo é a mesma coisa que menos o seno do mesmo ângulo só que com sinal positivo (ou seja, ).
Só mais uma coisa: o tem um intervalo específico pra ser válido, que é . Isso se dá porque, fora desse intervalo, a função deixa de ser injetora (quando dois senos forem iguais, os ângulos precisam ser iguais. E isso acontece em ) e ela tem que ser injetora porque as injetoras possuem uma função inversa e o é a função inversa do seno.
Agora que revisei isso com você, bora lá?
Passo 2
Sem mais delongas, vamos começar a questão.
O que o nosso problema quer é o , ou seja, o arco cujo seno vale . Antes de resolver, precisamos tirar essa raiz do denominador. Racionalizando a fração (ou seja, multiplicando em cima e embaixo por , chegamos em = . Agora, precisamos saber onde o seno vale , entre o intervalo . Nesse caso, é o 45° ().