Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.6 - Ex. 8b
Determine o valor exato da função .
Passo 1
Já vimos na questão anterior o círculo trigonométrico
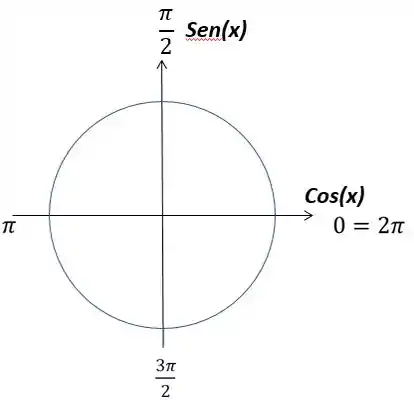
E também que “O cosseno é com sono, então ele fica deitado (eixo x ). O seno é sem sono, então ele fica em pé ( eixo y) ”. Então podemos seguir em frente. Vamos lembrar que cosseno é uma função par, isso quer dizer que :
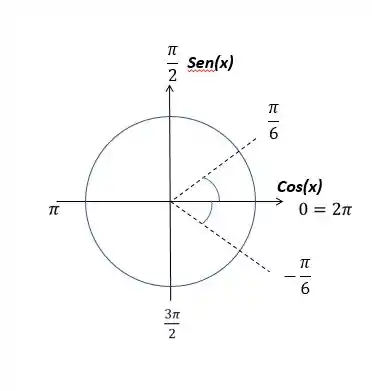
Olhar geometricamente sempre ajuda. O que é ótimo. Assim já conseguimos achar um ângulo igual no primeiro quadrante, logo de cara.
Passo 2
Pela tabela de funções trigonométrica temos:
Resposta
Exercícios de Livros Relacionados
Faça os gráficos das funções nos Exercícios 13-22. Qual o período de cada função? c o s( π x )
Nos exercícios 39-42, expresse a quantidade em termos de sen x e cos x .42. co s 3 π 2 + x
37. O que acontece se você tomar a identidade trigonométrica cos A - B = cos A cos B + sen A sen B ? O resultado se parece com algo que você conhece?
43. Avalie sen 7 π 12 como sen π 4 + π 3
Nos exercícios 39-42, expresse a quantidade em termos de sen x e cos x .39. cos ( π + x )