Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.Revisão - Ex. 65

Determine o valor exato da função

a ) sen (2 pi)/(3)

b ) cos (5 pi)/(4)

c ) tg (- (5 pi)/(6))

d ) cotg ((13 pi)/(12))

e ) sec pi

f ) cosec (- (pi)/(8))

Passo 1

Letra a .

Ele quer o seno do ângulo (2 pi)/(3) , a primeira coisa que temos que fazer é achar esse ponto nos quadrantes.

(2 pi)/(3) = 120 °

Colocando esse ponto no ciclo trigonométrico, vamos ter:

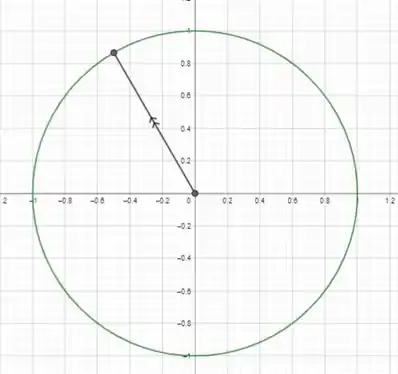
Opa, está no segundo quadrante, então o seno dele vai ser igual ao seno de quanto falta para chegar em 180 ° , que é fazer pi menos o nosso ângulo.

sen (2 pi)/(3) = sen (pi - (2 pi)/(3)) = sen (pi)/(3)

Lembrando que

(pi)/(3) = 60 °

sen (2 pi)/(3) = sen (pi)/(3) = (sqrt(3))/(2)

Passo 2

Letra b .

Ele quer o cosseno do ângulo (5 pi)/(4) , a primeira coisa que temos que fazer é achar esse ponto nos quadrantes.

(5 pi)/(4) = 225 °

Colocando esse ponto no ciclo trigonométrico, vamos ter:

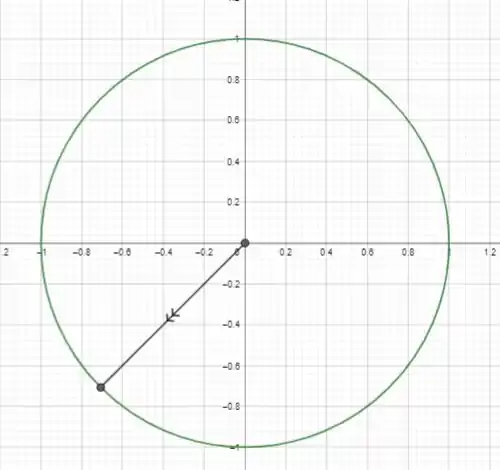
Opa, está no terceiro quadrante, então o cosseno dele vai ser igual à menos o cosseno de quanto passou de 180 ° , que é fazer o nosso ângulo menos pi

cos (5 pi)/(4) = - cos ((5 pi)/(4) - pi) = - cos (pi)/(4)

Lembrando que

(pi)/(4) = 45 °

cos (5 pi)/(4) = - cos (pi)/(4) = - (sqrt(2))/(2)

Passo 3

Letra c .

Ele quer a tangente do ângulo - (5 pi)/(6) , a primeira coisa que temos que fazer é achar esse ponto nos quadrantes.

- (5 pi)/(6) = - 150 °

Colocando esse ponto no ciclo trigonométrico, vamos ter:

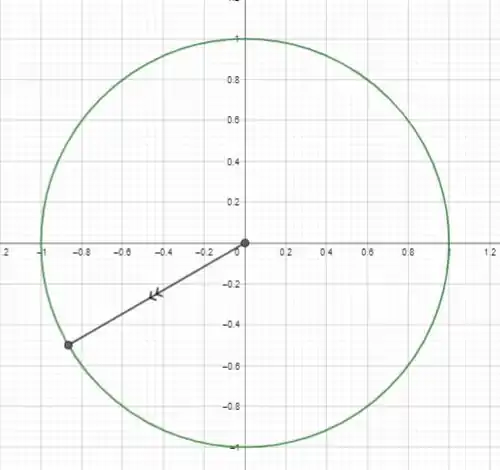
Opa, está no terceiro quadrante, então a tangente dele vai ser igual à tangente de quanto passou de 180 ° , como o ângulo é negativo devemos somar pi .

tg (- (5 pi)/(6)) = tg (- (5 pi)/(6) + pi) = tg (pi)/(6)

Lembrando que

(pi)/(6) = 30 °

tg (- (5 pi)/(6)) = tg (pi)/(6) = (sqrt(3))/(3)

Passo 4

Letra d .

Ele quer a cotangente do ângulo (13 pi)/(12) , a primeira coisa que temos que fazer é achar esse ponto nos quadrantes.

(13 pi)/(12) = 195 °

Colocando esse ponto no ciclo trigonométrico, vamos ter:

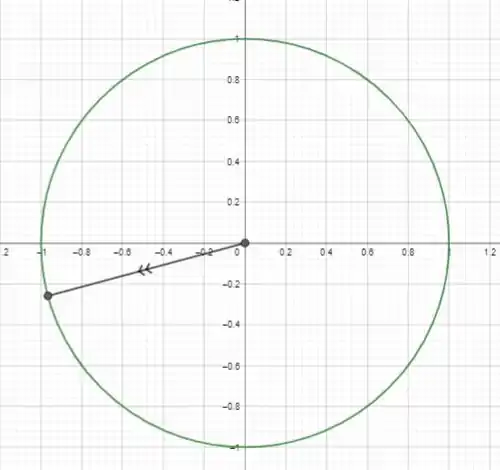
Opa, está no terceiro quadrante. Para analisarmos a cotangente, temos que ter em mente que:

cotg x = (1)/(tg x)

Então ela tem o mesmo comportamento da tangente.

A cotangente dele vai ser igual à cotangente de quanto passou 180 ° , que é fazer o nosso ângulo menos pi

cotg (13 pi)/(12) = cotg ((13 pi)/(12) - pi) = cotg (pi)/(12)

Lembrando que

(pi)/(12) = 15 °

Mas esse ângulo não é nenhum dos notáveis. O que fazer agora?

Temos que tentar achar 15 ° a partir de 30 ° , 45 ° , 60 ° .

Passo 5

Repare que:

15 ° = 45 ° - 30 °

Entao devemos fazer

cotg (pi)/(12) = cotg ((pi)/(4) - (pi)/(6)) = (1)/(tg ((pi)/(4) - (pi)/(6)))

Temos que:

tg ((pi)/(4) - (pi)/(6)) = (tg (pi)/(4) - tg (pi)/(6))/(1 + tg (pi)/(4) tg (pi)/(6)) = (1 - (sqrt(3))/(3))/(1 + 1 . (sqrt(3))/(3)) = (1 - (sqrt(3))/(3))/(1 + (sqrt(3))/(3)) = ((3 - sqrt(3))/(3))/((3 + sqrt(3))/(3)) = (3 - sqrt(3))/(3 + sqrt(3))

Logo:

cotg (13 pi)/(12) = cotg (pi)/(12) = (3 + sqrt(3))/(3 - sqrt(3))

Passo 6

Letra e .

sec pi

Ele quer a secante do ângulo pi , aqui não precisamos nos preocupar com que quadrante vamos ter, porque o pi é um ângulo notável.

Vamos lembrar que:

sec pi = (1)/(cos pi)

E

cos pi = - 1

Então:

sec pi = (1)/(cos pi) = (1)/(- 1) = - 1

Passo 7

Letra f .

Ele quer a cossecante do ângulo - (pi)/(8) , a primeira coisa que temos que fazer é achar esse ponto nos quadrantes.

- (pi)/(8) = - 22,5 °

Colocando esse ponto no ciclo trigonométrico, vamos ter:

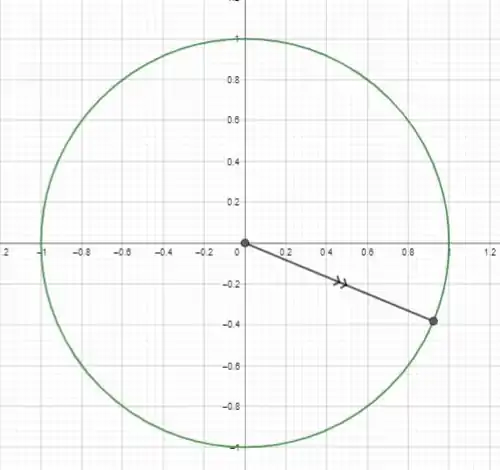
Opa, está no quarto quadrante.

Para analisarmos a cossecante, temos que ter em mente que:

co sec x = (1)/(sen x)

Então ela tem o mesmo comportamento do seno.

A cossecante dele vai ser igual à menos a cossecante de quanto falta para chegar em 360 ° , que é fazer 0 menos o nosso ângulo.

cosec (- (pi)/(8)) = - cosec (0 - (- (pi)/(8))) = - cosec ((pi)/(8))

Lembrando que

(pi)/(8) = 22,5 °

Mas esse ângulo não é nenhum dos notáveis. O que fazer agora?

Temos que tentar achar 22,5 ° a partir de 30 ° , 45 ° , 60 ° .

Passo 8

Repare que:

22,5 ° = (45 °)/(2)

Entao devemos usar:

cos 2 x = 1 - 2 sen^2 x

Usando x = (pi)/(8) , vamos ter:

cos (pi)/(4) = 1 - 2 sen^2 (pi)/(8)

(sqrt(2))/(2) = 1 - 2 sen^2 (pi)/(8)

2 sen^2 (pi)/(8) = 1 - (sqrt(2))/(2)

2 sen^2 (pi)/(8) = (2 - sqrt(2))/(2)

sen^2 (pi)/(8) = (2 - sqrt(2))/(4)

sen (pi)/(8) = sqrt((2 - sqrt(2))/(4))

sen (pi)/(8) = (sqrt(2 - sqrt(2)))/(2)

Temos que:

cosec (- (pi)/(8)) = - cosec ((pi)/(8)) = - (1)/(sen (pi)/(8)) = - (2)/(sqrt(2 - sqrt(2)))

Resposta

Letra a

sen (2 pi)/(3) = (sqrt(3))/(2)

Letra b

cos (5 pi)/(4) = - (sqrt(2))/(2)

Letra c

tg (- (5 pi)/(6)) = (sqrt(3))/(3)

Letra d

cotg (13 pi)/(12) = (3 + sqrt(3))/(3 - sqrt(3))

Letra e

sec pi = - 1

Letra f

cosec (- (pi)/(8)) = - (2)/(sqrt(2 - sqrt(2)))

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre todos os valores de t no intervalo [ 0,2 π ) em que a equação c o t g t = 1 está satisfeita.
Use a periodicidade das funções tangente e cotangente, bem como os valores do t g t , e c o t g ( t ) , quando 0 ≤ tπ , para determinar o valor exato da função t g - 11 4 π .
Use a periodicidade das funções tangente e cotangente, bem como os valores do t g t , e c o t g ( t ) , quando 0 ≤ tπ , para determinar o valor exato da função c o t g 15 2 π .
Encontre todos os valores de t no intervalo [ 0,2 π ) em que a equação s e n t = - 1 está satisfeita.
Encontre todos os valores de t no intervalo [ 0,2 π ) em que a equação c o s e c t = 1 está satisfeita.