Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.1 - Ex. 61
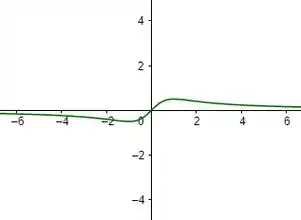
Determine os valores extremos (absoluto e local) das funções e onde ocorrem:
Passo 1
Sabendo que um ponto crítico é um valor extremo de uma função, a derivada da função deve ser igual a 0, uma vez que representa a inclinação de uma reta tangente que passa por esse ponto.
Encontrados os pontos críticos, é necessário ter noções do gráfico da função para classificá-los como máximo ou mínimo, global ou local.
Passo 2
Derivando pela regra do quociente, teremos:
Passo 3
Agora calculando :
Passo 4
Substituindo os pontos encontrados na função original:
Passo 5
Fazendo a análise do gráfico, teremos:
Resposta
Exercícios de Livros Relacionados
Determine os intervalos abertos em que a função é crescente e aqueles em que ela é decrescenteIdentifique os valores extremos absolutos e locais das funções, se houver, indicando onde ocorrem f θ = 6
Determine os intervalos abertos em que a função é crescente e aqueles em que ela é decrescenteIdentifique os valores extremos absolutos e locais das funções, se houver, indicando onde ocorrem h x =2 x
Determine os intervalos abertos em que a função é crescente e aqueles em que ela é decrescenteIdentifique os valores extremos absolutos e locais das funções, se houver, indicando onde ocorrem k t = 15
Determine os intervalos abertos em que a função é crescente e aqueles em que ela é decrescenteIdentifique os valores extremos absolutos e locais das funções, se houver, indicando onde ocorrem h r = r
Determine os intervalos abertos em que a função é crescente e aqueles em que ela é decrescenteIdentifique os valores extremos absolutos e locais das funções, se houver, indicando onde ocorrem