Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.1 - Ex. 66

  1. Use um gráfico para estimar os valores de máximo e mínimo absolutos da função com precisão de duas casas decimais.
  2. Use os cálculos para encontrar os valores de máximo e mínimo exatos

f x = e x 3 - x ,     - 1 ≤ x ≤ 0

Passo 1

Fala aí! tudo certinho?

Nesse problema foi dada a função

f x = e x 3 - x

E nosso objetivo é encontrar os valore de máximos e mínimos dessa função dentro do intervalo usando seu gráfico e por meio de cálculos.

- 1 ≤ x ≤ 0

Tem ideia de como fazemos isso?

Quando temos que determinar os pontos de máximos e mínimos de uma função em um intervalo contínuo e fechado temos que seguir um scriptzinho...

Primeiro obtemos os pontos críticos da função, pra isso derivamos a função e igualamos a 0 . Assim, os valores de x que satisfazem a igualdade será nossos pontos críticos.

Depois de obter os pontos críticos da função, excluímos os pontos que estiverem fora do intervalo da nossa análise e substituímos os pontos na função para comparar os valores das imagens e ver qual é o maior e o menor.

E por último, substituímos os limites do intervalo na função para comparar com as imagens dos pontos críticos...

Sacou? Bora começar!

Passo 2

Primeiro a questão pediu pra usarmos uma ferramenta gráfica para plotar o gráfico de f no intervalo e estimar seus máximos e mínimos.

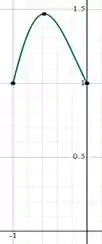
Pelo gráfico, podemos estimar que ( - 0,58   ,   1,47 ) é um ponto de máximo absoluto e os pontos de mínimo absoluto são os pontos ( - 1,1 ) e ( 0,1 )

Show?

Passo 3

Agora vamos obter esses valores por meio do scriptzinho que vimos no passo 1.

Derivando a função f pela regra da cadeia...

f x = e x 3 - x → f ' x = d x 3 - x d x · d e u d u

f ' x = 3 x 2 - 1 · e u

f ' x = 3 x 2 - 1 e x 3 - x

Igualando f ' a 0 vamos obter os pontos críticos...

f ' x = 3 x 2 - 1 e x 3 - x = 0

O termo e x 3 - x nunca é igual a 0 , então podemos simplifica-lo dividindo os dois lados por ele

3 x 2 - 1 e x 3 - x e x 3 - x = 0 e x 3 - x

3 x 2 - 1 = 0

x 2 = 1 3

x = ± 1 3

Como nosso intervalo de analise é - 1 ≤ x ≤ 0 , então vamos descartar o resultado positivo e assim temos apenas um ponto crítico dado por x = - 1 3 .

Tranquilo até aqui?

Passo 4

Agora vamos substituir o ponto crítico que encontramos na função e comparar sua imagem com as imagens dos limites do intervalo.

Para x = - 1 / 3 , temos

f - 1 3 = e - 1 3 3 - - 1 3 = e 2 3 9 ≈ 1,469

Para x = 0 ...

f 0 = e 0 3 - 0 = 1

E para x = - 1

f - 1 = e - 1 3 - - 1 = e 0 = 1

Assim, comparando os resultados, vemos que f - 1 3 = 1,469 é um ponto de máximo e os pontos f 0 = f - 1 = 1 são os pontos de mínimo.

É isso aí! o que achou? Responde Aí!

Resposta

f - 1 3 = 1,469 é um ponto de máximo e os pontos f 0 = f - 1 = 1 são os pontos de mínimo.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine os valores máximos e mínimos (caso existam) da função dada, no intervalo dado. g x = x 3 - 3 x 2 + 3 x - 1 em [ - 2 ,1 ]
Determine os valores máximos e mínimos (caso existam) da função dada, no intervalo dado. f x = x 5 5 - x 4 2 - x 3 + 4 x 2 - 4 x + 1 em [ - 3 ,3 ]
Determine os valores máximos e mínimos (caso existam) da função dada, no intervalo dado. f x = 1 x 3 - 2 x 2 em ] 0 ,2 [
Determine os valores máximos e mínimos (caso existam) da função dada, no intervalo dado. f x = x 4 4 - x 3 - 2 x 2 + 3 em [ - 2 ,3 ]
Determine os intervalos abertos em que a função é crescente e aqueles em que ela é decrescenteIdentifique os valores extremos absolutos e locais das funções, se houver, indicando onde ocorrem