Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.7 - Ex. 8

Determine os valores máximos e mínimos locais e pontos de sela da função. Se você tiver um programa para traçar gráficos tridimensionais no coputador, trace a função com um domínio e um ponto de vista que mostrem os seus aspctos importantes.

f x , y = e 4 y - x 2 - y 2

Passo 1

Opa, tudo tranquilo? Vamos lá responder essa questão! O enunciado nos dá a função

f x , y = e 4 y - x 2 - y 2

A ideia vai ser calcularmos as derivadas parciais da expressão, depois igualando f x   e     f y a 0 encontramos os pontos críticos. Através da fórmula:

D x , y = f x x ⋅ f y y - f x y x , y ²

E do teste da segunda derivada conseguimos descobrir se o ponto é máximo local, mínimo local ou ponto de sela.

Passo 2

Seja

f x , y =   e 4 y - x 2 - y 2

Pra começar, vamos ver como fica f x :

f x = - 2 x e 4 y - x 2 - y 2  

Para acharmos o f x x basta derivamos novamente em relação a x . usando a regra do produto, temos:

f x x = - 2 e 4 y - x 2 - y 2 + 4 x 2 e 4 y - x 2 - y 2

Repare que na formula do Passo 1, temos o termo f x y . Então vamos encontra-lo! Derivando em relação a y o termo f x :

f x y = - 2 x ( 4 - 2 y ) e 4 y - x 2 - y 2

Para acharmo o f y o processo é bem parecido, olha só:

f y = ( 4 - 2 y ) e 4 y - x 2 - y 2

Usando a regra do produto, conseguimos achar o f y y :

f y y = ( 4 y 2 - 16 y + 14 ) e 4 y - x 2 - y 2

Passo 3

Para acharmos os pontos de máximos e mínimos locais e pontos de sela da função, vamos igualar f x e f y a zero. Vem comigo!

f x = 0

- 2 x e 4 y - x 2 - y 2 = 0

Como o termo e 4 y - x 2 - y 2 é sempre positivo. Então:

x = 0

Agora vamos ver quando f y = 0

4 - 2 y e 4 y - x 2 - y 2 = 0

Aqui é a mesma coisa, como o termo e 4 y - x 2 - y 2 > 0 :

4 - 2 y = 0 → y = 2

Então temos apenas um ponto crítico que será o ( 0,2 ) .

Passo 4

Agora vamos verificar o que esse ponto representa.

D x , y = f x x ⋅ f y y - f x y x , y ²

Para o ponto ( 0,2 ) :

D 0,2 = f x x ( 0,2 ) ⋅ f y y ( 0,2 ) - f x y ( 0,2 ) 2

Do Passo 2:

f x x x , y = - 2 e 4 y - x 2 - y 2 + 4 x 2 e 4 y - x 2 - y 2

f y y ( x , y ) = 4 y 2 - 16 y + 14 e 4 y - x 2 - y 2

f x y = - 2 x ( 4 - 2 y ) e 4 y - x 2 - y 2

Substituindo o ponto ( 0,2 ) e fazendo as contas:

f x x 0,2 = - 2 e 4

f y y 0,2 = - 2 e 4

f x y 0,2 = 0

logo,

D 0,2 = - 2 e 4 ⋅ - 2 e 4 - 0 2 = 4 e 8 > 0

f x x 0,2 = - 2 e 4 < 0

Logo, f 0,2 = e 4 é um máximo local.

Passo 5

Fazendo um gráfico, temos:

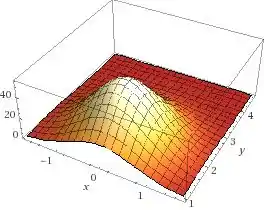
O que ilustra o ponto de máximo.

Resposta

O único ponto crítico é ( 0,2 ) e é um máximo local

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine os valores máximos e mínimos locais e pontos de sela da função. Se você tiver um programa de computador para desenhar em três dimensões, trace o gráfico da função usando um ponto de vista e
Determine os valores máximos e mínimos locais e pontos de dela da função. f x , y = x 4 + y 4 - 4 x y + 2
Determine os valores máximos e mínimos locais e pontos de sela da função. f x , y = ( x - y ) ( 1 - x y )