Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 14.7 - Ex. 14

Determine os valores máximos e mínimos locais e pontos de sela da função. Se você tiver um programa de computador para desenhar em três dimensões, trace o gráfico da função usando um ponto de vista e domínio convenientes para mostrar os aspectos importantes da função

f x , y = y cos ⁡ x

Passo 1

Eaee, belezinha?? Bom... o enunciado nos deu a seguinte função:

f x , y = y cos ⁡ x

Queremos determinar os valores de máximos e mínimos locais.

Para isso, precisamos fazer as derivadas parciais com relação à x e y e igualar os seus resultados a zero para encontrarmos os pontos críticos.

Em seguida, iremos fazer as segundas derivadas parciais f x x ,   f x y ,   f y y e aplicar na seguinte expressão (chamada de teste da segunda derivada):

D x , y = f x x ⋅ f y y - f x y x , y 2

Com isso, a gente analisa as seguintes proposições:

  • Se D > 0 e f x x x , y > 0 , então f x , y é um mínimo local;
  • Se D > 0 e f x x x , y < 0 , então f x , y é um máximo local;
  • Se D < 0 , não é nem máximo e nem mínimo local.

Em relação ao gráfico, iremos utilizar o GeoGebra para plotarmos o gráfico dessa função.

Passo 2

Vamos encontrar aqui então as deriadas parciais:

f x , y = y cos ⁡ x

Primeira derivada parcial em relação a x :

f x = - y s e n x

Agora a gente deriva em relação a x essa derivada que encontramos:

f x x = - y   c o s x

Agora a gente vai encontrar a derivada parcial em relação a y :

f y = c o s x

E novamente iremos calcular a derivada parcial em relação a y :

f y y = 0

Por ultimo iremos calcular a derivada parcial de f x em relação a y :

f x y = - s e n x

Passo 3

Agora que calculamos todas as derivadas parciais iremos em busca dos pontos críticos, para isso, deveremos encontrar os pontos f x = 0 e f y = 0 .

f x = - y s e n x

f x = 0 implica em y = 0   ou sin ⁡ x = 0 ( x = n π ,   n ∈   Ζ )

Já para:

f y = c o s x

f y = 0 implica em c o s x = 0 , logo x = n π + π 2 ,   n   ∈   Ζ

Logo, os pontos críticos devem ser ( n π + π 2 , 0 ) . Agora vamos avaliar esse ponto critico em D .

Assim,

D n π + π 2 , 0 = - y cos ⁡ x ⋅ 0 - - s e n x 2 = - s e n 2 x < 0

logo todos os pontos críticos são pontos de sela.

Podemos ver esse comportamento no gráfico gerado no GeoGebra:

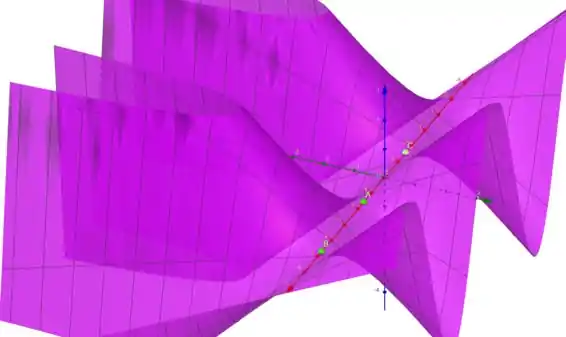
Resposta

Todos os pontos críticos são pontos de sela.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

38. Para as funções de uma variável, é impossível uma função continua ter dois pontos de máximo local e nenhum ponto de mínimo local. Para funções de duas variáveis, esse caso existe. Mostre que a fun
Utilize uma ferramenta gráfica como no Exemplo 4 (ou o Método de Newton ou um determinador de raízes) para encontrar os pontos críticos de f com precisão de três casas decimais. Em seguida, classifiqu
Mostre que f x ,y = x 2 + 4 y 2 - 4 x y + 2 tem um número infinito de pontos críticos e que D = 0 em cada um. A seguir, mostre que f tem um mínimo local (e absoluto) em cada ponto crítico.
5-20. Determine os valores máximos e mínimos locais e pontos de sela da função. Se você tiver um programa de computador para desenhar em três dimensões, trace o gráfico da função usando um ponto de vi
5-20. Determine os valores máximos e mínimos locais e pontos de sela da função. Se você tiver um programa de computador para desenhar em três dimensões, trace o gráfico da função usando um ponto de vi