Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 12.2 - Ex. 9
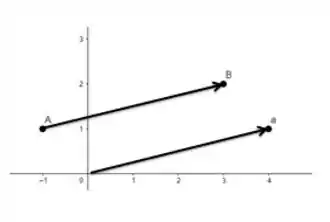
Determine o vetor com representação dada pelo segmento de reta orientado . Desenhe e o equivalente com início na origem.
Passo 1
Para resolvermos esse problema, temos que subtrair um ponto pelo outro, assim teremos um outro vetor.
Vamos lá!
Pronto! Temos o nosso vetor , agora vamos representá-lo graficamente:
Resposta
Exercícios de Livros Relacionados
Prove que u ∙ v =± u v se, e somente se, um dos vetores u, v é múltiplo do outro. Em seguida, compare u + v 2 = ( u + v∙ u + v ) com u + v 2 para concluir que u + v = u + | v | se, e somente se, um do
Dados u → = - x - 1,2 , 1 , v → = - 3 , x , 1ew → = x - 4,0 , 1 , determine x para que os vetores u → ,v →ew → sejam coplanares e dois a dois não paralelos. Para esse valor de x , escreva w → como com
Sabendo que os vetores a → , b →ec → são l . i . , determine o menor m tal que u → = a → + b → + c → , v → = 4 a → + m b → + c → e w → = b → + m c → sejam l . d . Com esse m , escreva t → = a → - b →
Sejam u → = m , - 1 , m 2 + 1 , v → = ( m 2 + 1 , m , 0 ) e w → = m , 1,1 . Mostre que C = ( u → , v → , w → ) é uma base de V , independentemente do valor de m .
Seja E = e → 1 , e → 2 , e → 3 uma base . Sejam f 1 → = e → 1 - e → 2 + e → 3 , f 2 → = e → 2 + e → 3 e f 3 → = - 2 e → 3 (b)Resolva x , y , z E = 3 , - 2,4 F .