Determine, aproximando o valor até a precisão de um grau, os três ângulos do triângulo cujos vértices são dados.
Passo 1
Vamos dizer que cada letra minúscula seja nosso vértice, okay? Certo! Desse modo, , são os vértices de , como mostra a figura:
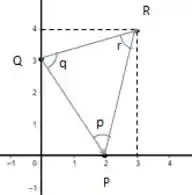
Então é o ângulo entre os vetores e ; é o ângulo entre os vetores e , e é o ângulo entre os vetores e .
Passo 2
Fazemos o ângulo de cada vetor. Para :
A mesma coisa serve para os outros. Para :
De uma maneira mais pratica podemos ter o valor do ângulo , uma vez que já temos os outros dois! Tendo em vista que esse triângulo compõe , podemos apenas subtrair do somatório dos ângulos que temos:
Finish!!
Resposta
, e .