40. (a) Como se deve estender f, definida originalmente em , de modo a se obter uma série de Fourier envolvendo apenas as funções , , , ? Veja os Problemas 38 e 39.
(b) Se para , esboce a função para a qual essa série de Fourier converge para .
Passo 1
Fala Galera!!!
Nosso objetivo nessa questão é obter uma série de Fourier contendo apenas termos de cosseno, para isso, a extensão de deve ser uma função par. Também queremos obter uma série contendo apenas os termos
Passo 2
Podemos observe que as funções são simétricas em relação a . Portanto, temos o seguinte:
Portanto, se for estendido para como uma função antissimétrica em torno de , isto é, para , então
Isso decorre do fato de que a integral de uma função antissimétrica em torno de . Portanto, agora podemos estender a função para obter
Finalmente, podemos estender a função resultante para como uma função par e, em seguida, como uma função periódica de período . Assim, por construção, a série de Fourier conterá apenas termos de cosseno. Então, primeiro notamos que:
Para , temos o seguinte:
Para a segunda integral, seja . Então nós temos
e, portanto, temos
Portanto, sabemos que
Segue-se imediatamente que a para ,
Assim, a representação da série de Fourier associada é a seguinte:
Em que a série converge quase em toda parte em e, portanto, em .
Passo 3
(b) Para a série encontrada acima em que para , o gráfico da função para a qual essa série de Fourier converge para é o seguinte:
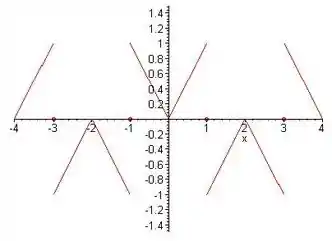
Resposta
Ei, a resposta está no passo a passo :)